domenica, 20 Aprile 2025
PetarKaran.it

Aruba, errore FTP 550 Can’t read directory: access denied

Problema: utilizzando FileZilla non si riesce a connettersi al server web su Aruba

Soluzione: aggiungere il proprio indirizzo IP agli IP autorizzati all’accesso via FTP dal panello di controllo

Per molti server Aruba ha attivo un servizio di filtro FTP che impedisce accessi non autorizzati, servizio molto utile per implementare il livello di sicurezza su uno dei protocolli più bucati di sempre.

Per aggiungere il proprio indirizzo IP a quelli autorizzati è sufficiente recarsi nel panello di controllo di Aruba.

Una volta dentro selezionare Gestione Accessi FTP.

Si presenterà una schermata simile a questa:

Premiamo su Abilita all’accesso FTP (questo abiliterà l’indirizzo IP mostrato che è anche quello da cui ci stiamo collegando). Altrimenti possiamo aggiungere manualmente un indirizzo IP cliccando poi su Aggiungi IP.

Dopodiché premiamo su Salva ed il gioco è fatto.

Adesso possiamo collegarci in FTP al nostro hosting.

[linux] Cercare testo dentro ai file in modo ricorsivo

Problema: Vogliamo cercare una porzione di testo dentro a tutti i file in una cartella e in tutte le sottocartelle

Soluzione: è sufficiente utilizzare il comando grep, nel modo seguente

Il parametro -R effettuerà una ricerca ricorsiva in tutte le sottocartelle, tra virgolette inseriamo il testo da cercare, il . (punto) indica che la ricerca debba cominciare dalla cartella corrente. 

Possiamo ovviamente indicare altre cartelle con:

 

Quanta energia consuma un PC in un anno?

Vi siete mai chiesti quanta energia consuma in media un computer all’anno? Chiaramente il consumo dipende sia dall’utilizzo che dalla potenza dell’alimentatore; per essere precisi un classico alimentatore da 450/500W non consuma energia sempre alla massima potenza, ma in base al carico computazionale sulla macchina. Per esempio se si gioca ad un videogioco si consuma più energia che se il computer rimane in stand-by.

Nel mio caso specifico lascio il computer di casa acceso anche quando non lo uso, spesso per compilare programmi o essere semplicemente disponibile da remoto.

In pratica questi sono i dati di un computer che è stato acceso per 365 giorni 24 ore al giorno. Per il calcolo del costo è stato utilizzato un parametro di 0,14 €/kWh.

Chiaramente questo risultato non sarà identico per tutti, ma possiamo dire che in media un computer lasciato acceso tutto il giorno ed utilizzato in modo mediamente intensivo consumi circa 500kWh all’anno, oppure circa 40kWh al mese.

Per confronto di seguito riporto invece i dati di un server Dell PowerEdge T110II (Intel® Xeon® Processor E31270v2, 4C/8T, 3.50GHz, 8M Cache, 69W, Turbo; 16GB Memory (2x8GB) 1600Mhz Dual; 2TB, SATA, 3.5in, 7.2K RPM) che gestisce un dominio con 15 utenti con funzionalità principale di server dati.

Anche in questo caso il server è rimasto acceso per 365 giorni 24 ore al giorno. Il consumo totale è stato di 270,15 kWh.

In pratica giocare ai videogiochi costa più che gestire una piccola rete aziendale! 

[joomla] Errore ERR_CONTENT_DECODING_FAILED su Chrome in Joomla 3.x

Problema: Quando si tenta di effettuare il login dal frontend si incorre nell’errore ERR_CONTENT_DECODING_FAILED su Chrome, mentre la pagina appare tutta bianca

Soluzione: disabilitare la compressione GZIP e pulire la cache

Quando si tenta di effettuare il login dal frontend di Joomla si potrebbe incorrere in una pagina vuota oppure nell’errore ERR_CONTENT_DECODING_FAILED. Cancellando l’URL e tornando alla homepage il login risulta effettuato e si può tornare a navigare.

Per risolvere il problema dovrebbe essere sufficiente disabilitare la compressione GZIP andando su Sistema > Configurazione globale > Server.

A questo punto andiamo su Sitema > Pulisci cache, selezioniamo tutte le voci e poi premiamo su Elimina.

Fatto tutto questo il problema dovrebbe risultare risolto.

[windows] Programmare spegnimento automatico ad una determinata ora

Obiettivo: Programmare lo spegnimento automatico del computer ad una determinata ora, per esempio alle ore 20 tutti i giorni.

All’interno di Windows è possibile configurare delle attività programmate. Per farlo clicchiamo col destro sul tasto Start e selezioniamo Gestione computer.

Spostiamo su Utilità di pianificazione e poi tra le opzioni a destra scegliamo Crea attività di base.

Seguiamo la procedura guidata e diamo un nome alla nostra pianificazione, per esempio “Spegnimento automatico ore 20”

Scegliamo quando attivare l’attività, per esempio Ogni giorno.

A questo punto ci verrà chiesta la data e l’ora, nonché il numero di ricorrenze.

Scegliamo avvio programma dalla schermata successiva.

A questo punto selezioniamo il programma shutdown.exe e passiamogli il parametro -s. 

Il parametro -s avvierà lo spegnimento entro 60 secondi dall’esecuzione, altrimenti possiamo impostare lo spegnimento ad un tempo prefissato con il parametro -t, per esempio -t 30 per avviare lo spegnimento entro 30 secondi, o -t 0 per avviarlo immediatamente.

Premiamo avanti e poi fine.

 

[WordPress] Creare un’area widget personalizzata in 6 semplici passaggi

Le aree dei widget in WordPress dipendono sempre dal template utilizzato, quindi per aggiungere un’area widget personalizzata bisogna modificare il template specifico che ci interessa.

Prima di cominciare procuriamoci tutto il necessario:

  1. Avere installato WordPress (lo si può scaricare da qui)
  2. Utilizziamo il template Twenty Sixteen (ricordo che la procedura è valida per qualunque template)

Se abbiamo tutto pronto cominciamo.

1. Apriamo l’editor di WordPress

L’editor si trova in Bacheca > Aspetto > Editor.

2. Andiamo su functions.php

Una volta aperto l’editor andiamo su functions.php, selezionabile dall’elenco a destra.

A questo punto spostiamoci in fondo al file e aggiungiamo il seguente codice:

Faccio notare come il nome della funzione, nuovo_widget(), è assolutamente arbitrario, purché rispetti i parametri di programmazione in PHP.

Dentro eseguiamo il metodo register_sidebar che permette di definire una specifica sidebar.

I parametri passabili tramite array sono:

  • name – il nome della sidebar, un testo descrittivo
  • description – la descrizione della sidebar, che apparirà sotto il suo nome nella bacheca, non è obbligatorio
  • id – identificativo della sidebar, deve essere tutto minuscolo e senza spazi, di predefinito è un valore numerico intero autoincrementale
  • before_widget – codice HTML da anteporre ad ogni widget
  • after_widget – codice HTML da posporre ad ogni widget
  • before_title – codice HTML da anteporre ad ogni titolo di widget
  • after_title – codice HTML da posporre ad ogni titolo di widget

Una volta aggiunto il codice premiamo su Aggiorna file.

3. Andiamo su page.php

Adesso aggiungiamo il widget in tutte le posizioni che desideriamo. Nel nostro caso lo aggiungeremo sul lato sinistro di tutte le pagine, modificabili da file page.php

Andiamo quindi a modificare il file page.php

Individuiamo la riga con get_header(); e posizioniamoci alla riga successiva aggiungendo il seguente codice:

Ricordiamoci che nuova-sidebar è l’ID che abbiamo definito prima per la nostra sidebar, mentre la classe barra-sinistra la dovremo ancora definire.

Individuiamo la riga con:

E modifichiamola nel modo seguente:

In questo modo il contenitore principale sarà modificato in base alla presenza o meno del widget. La situazione di partenza era questa:

Noi vogliamo arrivare ad una nuova situazione simile a questa:

4. Modifichiamo il style.css

Adesso non ci resta che aggiungere gli stili appena utilizzati. Andiamo quindi a modificare il Foglio di stile (style.css)

In fondo al file aggiungiamo le seguenti due righe di CSS (queste sono molto essenziali, per ottenere un risultato migliore bisognerebbe rielaborarle un po’).

Salviamo il file.

5. Andiamo sui Widget

Adesso è il momento di testare il nostro nuovo widget, spostiamoci perciò nei widget ed inseriamo nella nuova area, per esempio, il widget per la ricerca.

6. Risultato

A questo punto possiamo aprire il nostro sito e verificare il risultato, che dovrebbe apparire così.

[CCNA] Subnetting di una rete di classe B utilizzando i numeri binari

Proseguendo sulla falsa riga dell’esercizio precedente, dove avevamo calcolato le subnet per una rete di Classe C, supponiamo questa volta di avere l’indirizzo 172.24.0.0/16 e voler creare 10 subnet.

Vediamo quali saranno gli schemi IP dei numeri di broadcast, di rete e del numero di host, nonché la subnet mask.

1. Calcoliamo anzitutto il numero di subnet necessarie

In questo caso abbiamo un indirizzo di Classe B, quindi il suo schema potrebbe essere rappresentato nel modo seguente: NNNNNNNN . NNNNNNNN . HHHHHHHH . HHHHHHHH

A differenza del precedente esercizio, qui abbiamo 16 bit su H da cui possiamo prestare i bit per le nostre subnet. Come al solito il numero di subnet valide sarà dato da 2^N-2

Se prendessimo in prestito 2 H trasformandoli in N (ottenendo quindi il seguente schema NNNNNNNN . NNNNNNNN . NNHHHHHH . HHHHHHHH) potremmo realizzare 2^2-2 = 4 - 2 = 2 subnet

Faccio notare che con 1 H potremmo creare solo 2 subnet non valide.

Siccome vogliamo realizzare almeno 10 subnet, ci serve un numero di subnet tale che 2^N-2 \ge 10 ovvero dobbiamo prendere in prestito 4 H da trasformare in N, nel modo seguente: NNNNNNNN . NNNNNNNN . NNNNHHHH . HHHHHHHH

2. Determiniamo la prima subnet valida

A questo punto lavoriamo sullo schema precedente, dal momento che i primi due ottetti resteranno fissi, prendiamo in considerazione solo gli ultimi due: NNNNHHHH . HHHHHHHH

La prima subnet valida sarà quindi: 0001HHHH . HHHHHHHH

Vi ricordo che la 0000HHHH . HHHHHHHH non è valida dal momento che l’ID della subnet coinciderebbe con l’ID di rete.

Schematizzando il tutto avremo quindi:

ID prima sottorete 00010000 . 00000000 16 . 0 172.24.16.0
Primo host valido 00010000 . 00000001 16 . 1 172.24.16.1
Ultimo host valido 00011111 . 11111110 31 . 254 172.24.31.254
Broadcast prima sottorete 00011111 . 11111111 31 . 255 172.24.31.255

Come è facile notare basta riempire di 0 gli H dell’ID di sottorete, tutti 0 e un ultimo 1 per il primo host e via discorrendo. 

3. Determiniamo l’ultima subnet valida

In maniera analoga al punto precedente, determiniamo ora l’ultima subnet. Prendiamo lo schema e sostituiamo agli N la sequenza 1110 (vi ricordo che la 1111 porterebbe ad un broadcast non valido rispetto alla rete stessa)

L’ultima subnet sarà quindi: 1110HHHH . HHHHHHHH

A questo punto non ci rimane che calcolare il resto, con il medesimo procedimento di poco fa.

Schematizzando il tutto avremo quindi:

ID ultima sottorete 11100000 . 00000000 224 . 0 172.24.224.0
Primo host valido 11100000 . 00000001 224 . 1 172.24.224.1
Ultimo host valido 11101111 . 11111110 239 . 254 172.24.239.254
Broadcast prima sottorete 11101111 . 11111111 239 . 255 172.24.239.255

4. Determiniamo tutte le subnet valide

Come è facile immaginare basta ripetere gli schemi in rosso per tutte le varianti degli N in verde, cioè da 0001 a 1110 (ricordo che la somma binaria procede come 0001, 0010, 0011, 0100, ecc.).

Lo schema che otterremo sarà il seguente:

Subnet ID Rete Primo host Ultimo host Broadcast
0 (non valido) 172.24.0.0 172.24.0.1 172.24.0.254 172.24.15.255
1 172.24.16.0 172.24.16.1 172.24.16.254 172.24.31.255
2 172.24.32.0 172.24.32.1 172.24.32.254 172.24.47.255
3 172.24.48.0 172.24.48.1 172.24.48.254 172.24.63.255
4 172.24.64.0 172.24.64.1 172.24.64.254 172.24.79.255
5 172.24.80.0 172.24.80.1 172.24.80.254 172.24.95.255
6 172.24.96.0 172.24.96.1 172.24.96.254 172.24.111.255
7 172.24.112.0 172.24.112.1 172.24.112.254 172.24.127.255
8 172.24.128.0 172.24.128.1 172.24.128.254 172.24.143.255
9 172.24.144.0 172.24.144.1 172.24.144.254 172.24.159.255
10 172.24.160.0 172.24.160.1 172.24.160.254 172.24.175.255
11 172.24.176.0 172.24.176.1 172.24.176.254 172.24.191.255
12 172.24.192.0 172.24.192.1 172.24.192.254 172.24.207.255
13 172.24.208.0 172.24.208.1 172.24.208.254 172.24.223.255
14 172.24.224.0 172.24.224.1 172.24.224.254 172.24.239.255
15 (non valido) 172.24.240.0 172.24.240.1 172.24.240.254 172.24.255.255

Faccio notare come in questo caso tutti gli ID di rete siano a .0, mentre il terzo ottetto procede con lo stesso schema del quarto ottetto della classe C.

5. Determiniamo la subnet mask

Come nel caso precedente riprendiamo lo schema sul quale abbiamo realizzato le subnet: NNNNNNNN . NNNNNNNN . NNNNHHHH . HHHHHHHH

Agli N sostituiamo gli 1 e agli H sostituiamo gli 0: 11111111 . 11111111 . 11110000 . 00000000

Traducendo gli ottetti binari otteniamo quindi: 255.255.240.0

Questa sarà la nostra subnet mask. Ricordiamoci che siccome abbiamo in tutto 20 uni, la subnet è rappresentabile anche con /20

Nello specifico la prima subnet potremmo rappresentarla come 172.24.16.0/20 mentre l’ultima subnet sarebbe 172.24.224.0/20

[CCNA] Creare subnet in meno di un minuto (The Enhaced Bob Maneuver)

Oggi vediamo l’utilizzo di un metodo avanzato di subnetting proposto da Scott Empson. A quanto pare l’ideatore di questo metodo era un certo Bob, da cui il nome, manager/istruttore presso SHL.

Il metodo consiste nell’utilizzo della seguente tabella:

Vediamo come usarla per creare 9 subnet su una rete di Classe C, per esempio sull’indirizzo 192.168.1.0/24 come nel precedente esercizio.

1. Anzitutto individuiamo il numero di subnet che vogliamo creare, per fare questo andiamo sull’ultima riga e cerchiamo il primo numero maggiore o uguale a quello desiderato. Quindi se vogliamo creare 9 subnet dobbiamo selezionare il 14.

2. A questo punto ci spostiamo verso l’alto nella riga Bit Place (Posizione dei bit) e troviamo il 4. La riga nera è detta “riga di ordine superiore”, se attraversate questa riga, dovrete invertire posizione. Quindi dal momento che ci spostavamo da destra a sinistra, adesso ci sposteremo da sinistra a destra.

3. Passiamo a questo punto alla riga Target Number (numero target) e partendo da sinistra contiamo verso destra un numero di colonne pari al numero di bit (4).

Raggiungiamo il numero 16.

4. Questo è il numero target per il quale dobbiamo contare, partendo da zero fino a raggiungere o superare 255. Bisogna fermarsi prima di 256. Quindi contando avremo:

0, 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240, 256 (questo no, abbiamo superato 255!)

Questi sono gli ID di rete cercati.

5. Come nell’esercizio precedente, ricordiamoci la seguente regola:

ID Rete Primo Host Ultimo Host Broadcast
n1 n1+1 n2-2 n2-1
n2 … … …

Dove n1 è il primo ID di rete, n2 è il secondo e così via. Nel caso del punto 4 il valore di n1 sarebbe 0, di n2 sarebbe 16, di n3 sarebbe 32 e via discorrendo.

Quindi possiamo completare l’intera tabella nel modo seguente:

ID Rete Primo Host Ultimo Host Broadcast
0 (non valida) 1 14 15
16 17 30 31
32 33 46 47
48 49 62 63
64 65 78 79
80 81 … …
…      
224 225 238 239
240 (non valida per via del broadcast) 241 254 255

Faccio notare che ci sono 14 (ehi! ma è il numero di prima) subnet valide (16 – 2).

6. Come ultimo passaggio spostiamoci sopra il numero di target per trovare la subnet mask.

Siccome stiamo calcolando le subnet per una rete di Classe C la subnet mask sarà 255.255.255.240

Come al solito scegliamo, delle 14 subnet, le 10 che preferiamo e ne lasciamo 4 per scopi futuri.

Facile no? 🙂

[CCNA] Subnetting di una rete di classe C utilizzando i numeri binari

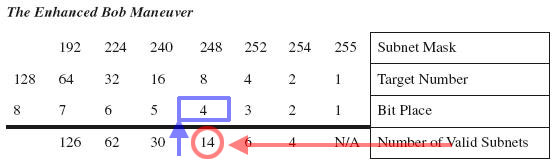
Immaginiamo di avere l’indirizzo 192.168.1.0/24 e di dover creare 10 nuove subnet.

Vediamo quali saranno gli schemi IP dei numeri di broadcast, di rete e del numero di host, nonché la subnet mask.

Questa parte teorica si rifà al calcolatore IP che potete trovare a questo link.

1. Calcolialiamo anzitutto il numero di subnet necessarie

Dal momento che le subnet vengono realizzate con i bit di coda dell’indirizzo IP non è possibile creare un qualsiasi numero di subnet, ma queste possono essere solamente potenze di 2.

In particolare le tre classi di indirizzi IP più comunemente utilizzate (A, B e C) hanno dei numeri predefiniti di bit dedicati alla rete (network) e i rimanenti ai host. Lo schema è il seguente:

Indirizzi di classe A N H H H
Indirizzi di classe B N N H H
Indirizzi di classe C N N N H

Dove N sono i bit di rete (network) e H i bit di host.

Questo significa che un indirizzo di classe C avrà i primi 3 ottetti di bit dedicati alla rete e l’ultimo ottetto ai host, da cui potremo ricavare le eventuali sottoreti.

Più in particolare l’espressione binaria dell’indirizzo soprastante potrà essere rappresentata così:

N N N H
192 168 1 0
11000000 10101000 00000001 00000000

Un’altra rappresentazione abbastanza comune è la seguente: NNNNNNNN . NNNNNNNN . NNNNNNNN . HHHHHHHH

In questo caso mettiamo in evidenza quali sono i bit di host (H) liberi per la creazione di eventuali sottoreti.

Avendo 8 bit a disposizione il numero massimo di sottoreti che potremo creare sarà dato da 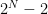2^N-2

Questo perché gli indirizzi iniziale e finale, ovvero 192.168.1.0 e 192.168.0.255 saranno rispettivamente l’id di rete ed il broadcast e quindi non sono validi ai fini della creazione di una sottorete.

Un’eventuale sottorete che partisse da 192.168.1.0 avrebbe infatti lo stesso ID di rete della rete principale!

Appurato questo abbiamo detto che vogliamo creare 10 sottoreti, ma essendo le sottoreti delle potenze di 2 possiamo crearle solo rispettando il seguente schema:

2^7 2^6 2^5 2^4 2^3 2^2 2^1 2^0
128 64 32 16 8 4 2 1

Di predefinito la rete 192.168.1.0/24 dispone di 8 bit liberi per i host, quindi H = 8 e N = 0, per quello che concerne le sottoreti, quindi di predefinito abbiamo 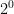2^0 sottoreti, ovvero una singola sottorete che poi è la rete principale.

Se prendessimo dagli H in prestito 3 bit N potremmo creare 8 sottoreti, che però non ci basterebbero, visto che ne vogliamo fare 10, quindi ne dobbiamo prendere 4. In questo modo avremo 14 sottoreti valide 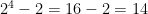2^4 - 2 = 16 - 2 = 14

Il prestito avviene per “espansione”, cioè estendiamo la notazione N. Quindi nel nostro schema precedente la situazione diventerebbe la seguente:

NNNNNNNN . NNNNNNNN . NNNNNNNN . NNNNHHHH

2. Determiniamo la prima subnet valida

Tenendo a mente lo schema NNNNHHHH adesso dobbiamo anzitutto calcolare il primo numero di sottorete.

Se contassimo in numeri decimali il primo numero sarebbero 0, ovvero 0000 in binario. Ricordiamoci che però questo non è valido (perché con N = 0000 e H = 0000 avremmo l’ID di sottorete uguale a quello della rete). Quindi partiamo da 1 e dunque 0001.

Sostituiamo allo schema precedente ed otteniamo 0001HHHH 

Adesso vogliamo calcolare l’ID di rete, ogni ID di sottorete comincia con 0, ovvero con 0000 nel nostro caso. In poche parole comincia con tutti gli H a zero.

Quindi avremo una situazione simile a 00010000

Il broadcast lo avremo sempre con tutti gli H a 1, quindi nel nostro caso a 1111. 

Il numero di broadcast sarà dunque 00011111

Il primo host valido della sottorete sarà il valore dell’ID di rete + 1, quindi 0000 + 0001 = 0001, mentre l’ultimo host sarà il valore di broadcast – 1, ovvero 1111 – 0001 = 1110 

Schematizzando il tutto quello che avremo sarà quanto segue:

ID prima sottorete 00010000 16 192.168.1.16
Primo host valido 00010001 17 192.168.1.17
Ultimo host valido 00011110 30 192.168.1.30
Broadcast prima sottorete 00011111 31 192.168.1.31

TRUCCO: L’ID di rete è sempre pari, il primo host è sempre dispari, l’ultimo host è sempre pari, il broadcast è sempre dispari!

3. Determiniamo l’ultima subnet valida

Avendo a mente lo schema NNNNHHHH, sappiamo che abbiamo 4 N per determinare la sottorete. L’ultima sottorete sarebbe quindi con N = 1111, ma questa non sarebbe valida, perché il suo broadcast, con tutti gli H a 1, coinciderebbe con quello della rete principale. Quindi l’ultima rete sarà con N = 1110.

A questo punto non ci rimane che ripetere il passaggio precedente, con l’unica differenza che la parte in verde anziché essere su 0001 sarà su 1110. Prendendo la tabella di prima il risultato sarà il seguente:

ID prima sottorete 11100000 224 192.168.1.224
Primo host valido 11100001 225 192.168.1.225
Ultimo host valido 11101110 238 192.168.1.238
Broadcast prima sottorete 11101111 239 192.168.1.239

4. Determiniamo l’elenco di tutte le subnet possibili

A questo punto non ci rimane che ripetere la procedura in modo automatizzato. Se siete degli sfaticati totali come il sottoscritto potete utilizzare un foglio excel per aiutarvi.

Da qui è possibile scaricarlo: Subnetting Classe C

Se lo preferite costruire da voi è sufficiente seguire la seguente procedura:

A1: IP

B1: 192.168.1.

A3: Subnet

B3: Subnet binario

C3: ID Rete

D3: Primo host

E3: Ultimo host

F3: Broadcast

A4: 0

B4: =DECIMALE.BINARIO(A4;4)

C4: =$B$1&BINARIO.DECIMALE(B4&”0000″)

D4: =$B$1&BINARIO.DECIMALE(B4&”0001″)

E4: =$B$1&BINARIO.DECIMALE(B4&”1110″)

F4: =$B$1&BINARIO.DECIMALE(B4&”1111″)

A5: =A4+1

Infine trascinate A5 fino a A19 e la riga B4:F4 fino a B19:F19.

Il risultato dovrebbe venire così:

Subnet Subnet binario ID Rete Primo host Ultimo host Broadcast
0 (non valido) 0000 192.168.1.0 192.168.1.1 192.168.1.14 192.168.1.15
1 0001 192.168.1.16 192.168.1.17 192.168.1.30 192.168.1.31
2 0010 192.168.1.32 192.168.1.33 192.168.1.46 192.168.1.47
3 0011 192.168.1.48 192.168.1.49 192.168.1.62 192.168.1.63
4 0100 192.168.1.64 192.168.1.65 192.168.1.78 192.168.1.79
5 0101 192.168.1.80 192.168.1.81 192.168.1.94 192.168.1.95
6 0110 192.168.1.96 192.168.1.97 192.168.1.110 192.168.1.111
7 0111 192.168.1.112 192.168.1.113 192.168.1.126 192.168.1.127
8 1000 192.168.1.128 192.168.1.129 192.168.1.142 192.168.1.143
9 1001 192.168.1.144 192.168.1.145 192.168.1.158 192.168.1.159
10 1010 192.168.1.160 192.168.1.161 192.168.1.174 192.168.1.175
11 1011 192.168.1.176 192.168.1.177 192.168.1.190 192.168.1.191
12 1100 192.168.1.192 192.168.1.193 192.168.1.206 192.168.1.207
13 1101 192.168.1.208 192.168.1.209 192.168.1.222 192.168.1.223
14 1110 192.168.1.224 192.168.1.225 192.168.1.238 192.168.1.239
15 (non valido) 1111 192.168.1.240 192.168.1.241 192.168.1.254 192.168.1.255

TRUCCO: Fate caso che vanno di 16 in 16? Questo perché abbiamo fatto subnetting con 2^4 = 16

5. Determiniamo la subnet mask

A questo punto non ci rimane che determinare la subnet mask, la cosa più facile in assoluto in questo caso.

Ricordiamo che il nostro schema è: NNNNNNNN . NNNNNNNN . NNNNNNNN . NNNNHHHH

Di predefinito la subnet mask per un indirizzo di Classe C è 255.255.255.0, ovvero 11111111.11111111.11111111.00000000

Nel nostro caso abbiamo preso in prestito 4 bit dai bit di host (H) e la subnet diventa: 11111111.11111111.11111111.11110000

Quindi 255.255.255.240 

Oppure /28, perché gli 1 sono 28 di 32. 

6. Conclusione

In principio noi volevamo creare 10 subnet diverse, a partire dalla rete 192.168.1.0/24

Abbiamo visto come possiamo creare 14 subnet, di cui ne sceglieremo 10 a piacere, 4 possono avanzarci per scopi futuri.

Il gruppo di subnet è rappresentabile da 192.168.1.0/28 e le subnet valide vanno dalla 192.168.1.16/28 alla 192.168.1.224/28.

In ognuna delle 14 subnet create (16 – 2) abbiamo  2^H-2 = 2^4 - 2 = 14 host validi.

[linux] Aggiungere file manualmente ad una condivisione su ownCloud (sotto Plesk)

Obiettivo: aggiungere un file manualmente nella partizione utente su ownCloud, senza utilizzare l’interfaccia di gestione

Questa è una soluzione molto interessante qualora si preferisca caricare il file, per svariati motivi, con altri meccanismi, diversi dall’interfaccia utente offerta dalla piattaforma ownCloud. Per esempio avevo bisogno di condividere un file zip di 600MB che però prima andava modificato. In tal caso, scaricarlo sul mio computer e caricarlo di nuovo online, con la connessione a 20 Mega, rischiava di risultare eccessivamente lento e macchinoso, quando potevo invece scaricarlo direttamente sul server e modificarlo da terminale.

Come fare allora per metterlo in condivisione?

L’operazione è semplice: anzitutto dobbiamo collocarci nella partizione dati di ownCloud e trovare la cartella, sotto files, dell’utente al quale vogliamo mettere a disposizione il file.

Una volta nella cartella digitiamo:

In questo modo visualizzeremo il dettaglio dei permessi sui file. Annotiamo utente e gruppo che accedono alla partizione.

Spostiamoci nella cartella di installazione di ownCloud, per esempio con:

Quello che ci interessa è la cartella, di ownCloud, contenente l’eseguibile occ.

A questo punto digitiamo il comando per ricostruire tutta la partizione dell’utente all’interno di ownCloud. Attenzione, questo comando reimposterà tutte le configurazioni delle cartelle su ownCloud gestite dall’utente.

Faccio notare che il nome_utente è l’utente proprietario dei file nella partizione linux, per esempio www-data se siamo sotto apache (lo vediamo con il comando precedente).

utente_owncloud è invece l’utente registrato in ownCloud, ovvero lo username dell’utente a cui appartiene la partizione.

In questo caso verrà utilizzato il PHP predefinito configurato all’interno di Linux, qualora voleste (o doveste) utilizzare un’altra versione, sarà sufficiente digitare il percorso per intero; ad esempio sotto Plesk i file binari del PHP7.0 si possono recuperare in questo modo:

Per maggiori informazioni e dettagli consiglio la pagina della documentazione ufficiale di ownCloud.