[excel] Calcolare tutte le possibili combinazioni con ripetizione usando le matrici in Excel

Obiettivo: dato un insieme di elementi distinti n vogliamo calcolare tutte le possibili combinazioni che si possono formare con k degli n elementi dati, dove

Secondo il calcolo combinatorio il numero di combinazioni con ripetizione che possiamo ottenere si calcola con la seguente formula:

Con Excel vogliamo ottenere una matrice contenente tutti gli elementi, dove ogni elemento può essere testuale o numerico. A tale scopo utilizzeremo le caratteristiche sul calcolo matriciale introdotte recentemente in Office365 e le seguenti funzioni: INDICE, INDIRETTO, MATR.TRASPOSTA, RIPETI, UNICI, STRINGA.ESTRAI, FILTRO

Prima di procedere ricordiamo che UNICI e FILTRO sono per ora disponibili solo con Office365. Inoltre useremo il # (cancelletto) nella costruzione dei riferimenti, per prendere gli intervalli dinamici generati dalle matrici.

Definiamo quindi anzitutto gli elementi n e il numero di ripetizioni k in questo modo:

Nella riga 1 potremo aggiungere altri elementi a piacere, mentre in B2 inseriremo il numero di ripetizioni desiderate. Per praticità ho chiamato gli elementi A, B e C.

Cominciamo allora calcolando anzitutto il numero di elemento n nella cella B3:

Adesso vogliamo determinare il numero di disposizioni con ripetizione possibili, ovvero tutti i modi in cui possiamo disporre gli n elementi presi a gruppi di k, dove conta l’ordine.

Per chi non fosse pratico dell’argomento se abbiamo i suddetti 3 elementi, allora nelle combinazioni con ripetizione ABC e ACB sono la stessa combinazione (contengono ciascuna tutti e 3 gli elementi), mentre nelle disposizioni con ripetizione ABC e ACB sono elementi distinti.

Il numero totale di disposizioni con ripetizione sarà dato dalla formula:

Che tradotta in Excel possiamo scrivere in B5 come:

Date queste informazioni calcoliamo tutti gli elementi possibili con la seguente formula in B11:

Questa genererà un risultato come il seguente:

L’idea è fondamentalmente quella di generare una matrice di riferimenti agli elementi dati in modo ordinato. Con 3 elementi presi 3 per volta avremo in tutto 27 disposizioni con ripetizione. Generiamo allora una matrice colonna con valori [1…27]. Nella prima colonna da [1…9] avremo il primo elemento, da [10…18] avremo il secondo elemento e così via. Siccome il primo elemento corrisponde a 1 e il secondo a 2, questo significa che presi i valori da [1…27] li dovremo dividere in 3 parti di 9 elementi ciascuna.

Questo lo potremmo ottenere scrivendo:

In questo modo generiamo [1…27] e dividiamo per 9, poi arrotondiamo per eccesso il risultato. Ne seguirà che, arrotondati per eccesso, 1/9 ⇒ 1, 9/9 ⇒ 1, 10/9 ⇒ 2, 18/9 ⇒ 2, 19/9 ⇒ 3, 27/9 ⇒ 3. Avremo insomma tre intervalli fatti, rispettivamente, di [1…1], [2…] e [3…3], ciascuno di 9 sottoelementi.

Nell’immagine di seguito vediamo la schematizzazione di ciò che vogliamo ottenere:

Per ciascun gruppo della prima colonna vorremo ottenere, nella seconda colonna, altri 3 sottogruppi, per ciascuno dei quali, nella terza colonna, vorremo ottenere altri 3 sottogruppi (questa volta di dimensione 1). Quindi i gruppi saranno 1, 3 e 9. Questi sono anche i valori per i quali dobbiamo sezionare gli intervalli delle colonne.

Per generare questi valori usiamo:

La matrice trasposta ci serve per metterli in riga, anziché in colonna. Dividiamo infine la prima colonna per questa riga.

Fatto questo spostiamoci in I10 e digitiamo:

In questo modo riportiamo semplicemente gli elementi scritti da B1 in poi.

In I11 calcoliamo quante volte appare ciascun elemento della matrice in B11#:

NB: grazie al cancelletto selezioniamo tutta la matrice generata da B11.

Il risultato che avremo sarà:

Nella prima riga A è presente 3 volte, gli altri due elementi 0 volte. Nella seconda riga abbiamo 2 A e 1 B, ecc.

In questo caso stiamo semplicemente usando la funzione CONTA.PIÙ.SE su righe successive, per ciascuno dei valori immessi.

A questo punto, sapendo quanti sono i singoli valori, possiamo usare la funzione RIPETI per riscriverli. Tale funzione ripete un dato valore per n volte. Quindi in P11 scriviamo:

Otterremo un risultato come il seguente:

Adesso facciamo una mossa un po’ astrusa. Siccome sappiamo che per ogni riga ci sono k elementi, ovvero 3 elementi, concateniamo tutta la matrice in una singola stringa e la spezziamo in pezzi da 3 elementi per volta. Verrà quindi una lunghissima stringa che comincerà con AAAAABAACAABABBABCAAC… e che verrà spezzata in AAA, AAB, AAC, AAB, ABB ecc.

Per farlo in W11 digitiamo:

La parte di formula con:

Genera una matrice colonna tipo:

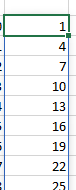
La usiamo per spezzare la stringa in parti da 3 a partire dal 1° carattere, il 4° carattere, il 7° carattere ecc.

Il risultato che otterremo saranno tutte le disposizioni con ripetizione di cui parlavamo prima:

Per ottenere le combinazioni con ripetizione che stavamo cercando possiamo fare in due modi.

1. Utilizzando la funzione UNICI

In Z11 scriviamo:

E ricaviamo immediatamente l’elenco ridotto delle combinazioni in questo modo:

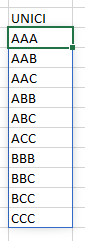
Questa è la maniera più semplice e veloce.

2. Utilizzando la funzione FILTRO

Questo è un modo un pizzico più complicato. Per ciascuno dei valori in W11# vogliamo calcolare la presenza del valore stesso nelle righe precedenti. Per farlo utilizzeremo la funzione SCARTO, aumentando la altezza della colonna della matrice di controllo via via che scendiamo. A questa applicheremo il CONTA.SE per vedere se il valore attuale, cioè ciascun valore della matrice, è presente nella sottomatrice precedente calcolata con SCARTO. Confrontando questo valore con 1, ovvero che debba comparire una sola volta, costruiremo la matrice colonna per il filtro da applicare alla funzione FILTRO.

La formula quindi sarà:

In entrambi i casi il risultato sarà identico:

Dal seguente link è possibile scaricare il file Excel con tutti i calcoli già fatti: combinazioni semplici