Quello che voglio realizzare oggi è un semplice programma in Python 2.7, con interfaccia grafica e che permetta di disegnare un poligono regolare dato il numero di lati. In questo esercizio vedremo quindi due cose:
- L’utilizzo di wxPython per creare un rudimentale programma con interfaccia grafica
- L’utilizzo di PyOpenGL per disegnare dentro ad un canvas una figura geometrica
Il programma che andremo a creare avrà alla fine questo aspetto, con uno spazio per inserire il numero di lati ed un canvas su cui disegnare:

Anzitutto assicuriamoci di disporre di entrambe le librerie, per farlo installiamole con pip eseguendo i seguenti due comandi da terminale:
|
1 2 |
pip install wxPython pip install PyOpenGL |
Una volta installate le librerie possiamo cominciare a creare il nostro programma.
Per prima cosa creiamo una classe per la nostra applicazione, utilizzando wx.Frame e avviando la finestra principale. Il codice di cui avremo bisogno sarà il seguente:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import wx class Applicazione(wx.Frame): def __init__(s, parent, title): wx.Frame.__init__(s, parent, title=title, size=(800,600)) s.Show(True) if __name__ == "__main__": app = wx.App(False) frame = Applicazione(None, "Disegnatore") app.MainLoop() |
In questo modo creiamo una finestra di dimensione 800 x 600 px con titolo Disegnatore. La nostra applicazione è un’estensione di wx.Frame, laddove un Frame è una finestra le cui dimensioni e posizione possono essere modificate dall’utente (insomma la classica finestra in Windows). Inoltre essa può contenere una barra del titolo, dei menu, dello stato e degli strumenti.
Con wx.App avviamo invece l’applicazione vera e propria, questa classe ci serve per lanciare il contenitore principale dell’applicazione e passiamo come argomento False (che sarebbe così anche di predefinito) per non reindirizzare lo sys.stdout e lo sys.stderr. Per maggiori informazioni rimando alla guida ufficiale su App.
A questo punto voglio aggiungere la casella di testo e il pulsante per impostare il numero di lati. Per farlo dobbiamo usare un wx.Panel, che sostanzialmente è il contenitore degli elementi di controllo e si trova tipicamente dentro un Frame. Per maggiori informazioni leggere qui su Panel.
Modifico quindi il codice nella maniera seguente:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
import wx class Applicazione(wx.Frame): def __init__(s, parent, title): wx.Frame.__init__(s, parent, title=title, size=(800,600)) # aggiungo un panel alla classe s.panel = wx.Panel(s) # dopo il panel aggiungo i pulsanti s.aggPulsanti() s.Show(True) def aggPulsanti(s): # casella di testo s.testo = wx.TextCtrl(s.panel, pos=(5, 7)) # pulsante s.pulsante = wx.Button(s.panel, label="Calcola", pos=(120,5)) if __name__ == "__main__": app = wx.App(False) frame = Applicazione(None, "Disegnatore") app.MainLoop() |
E’ molto importante che il Panel venga istanziato prima del metodo aggPulsanti che poi aggiunge elementi al Panel. Arrivati a questo punto lanciamo il nostro programma e verifichiamo che abbia il seguente aspetto.
A questo punto è l’ora di aggiungere anche il Canvas che ci permetterà di mostrare grafica in OpenGL. Per farlo includiamo anzitutto le librerie necessarie:
|
1 2 3 |
from wx.glcanvas import GLCanvas from OpenGL.GLU import * from OpenGL.GL import * |
Modifichiamo poi il codice nel modo seguente:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
import wx from wx.glcanvas import GLCanvas from OpenGL.GLU import * from OpenGL.GL import * class Applicazione(wx.Frame): def __init__(s, parent, title): wx.Frame.__init__(s, parent, title=title, size=(800,600)) # aggiungo un panel alla classe s.panel = wx.Panel(s) # dopo il panel aggiungo i pulsanti s.aggPulsanti() # stabiliamo le dimensioni del canvas s.width = 770 s.height = 500 # aggiungiamo il canvas, anche esso sul panel s.aggCanvas() s.Show(True) def aggPulsanti(s): # casella di testo s.testo = wx.TextCtrl(s.panel, pos=(5, 7)) # pulsante s.pulsante = wx.Button(s.panel, label="Calcola", pos=(120,5)) def aggCanvas(s): gl_canvas_attribs = [wx.glcanvas.WX_GL_RGBA, wx.glcanvas.WX_GL_DOUBLEBUFFER, wx.glcanvas.WX_GL_DEPTH_SIZE, 16] s.canvas = wx.glcanvas.GLCanvas(s.panel, attribList=gl_canvas_attribs, pos=(5,50)) s.context = wx.glcanvas.GLContext(s.canvas) s.canvas.SetSize((s.width,s.height)) if __name__ == "__main__": app = wx.App(False) frame = Applicazione(None, "Disegnatore") app.MainLoop() |
E’ importante stabilire le dimensioni del canvas in due variabili s.width e s.height per delle correzioni che apporteremo successivamente, per ora prendiamola per buona così.
A questo punto inizializziamo il canvas aggiungendo le seguenti istruzioni:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 |
import wx from wx.glcanvas import GLCanvas from OpenGL.GLU import * from OpenGL.GL import * class Applicazione(wx.Frame): def __init__(s, parent, title): wx.Frame.__init__(s, parent, title=title, size=(800,600)) # aggiungo un panel alla classe s.panel = wx.Panel(s) # dopo il panel aggiungo i pulsanti s.aggPulsanti() # stabiliamo le dimensioni del canvas s.width = 770 s.height = 500 # aggiungiamo il controllo di inizializzazione del canvas s.glInizializzato = False # aggiungiamo il canvas, anche esso sul panel s.aggCanvas() s.Show(True) def aggPulsanti(s): # casella di testo s.testo = wx.TextCtrl(s.panel, pos=(5, 7)) # pulsante s.pulsante = wx.Button(s.panel, label="Calcola", pos=(120,5)) def aggCanvas(s): gl_canvas_attribs = [wx.glcanvas.WX_GL_RGBA, wx.glcanvas.WX_GL_DOUBLEBUFFER, wx.glcanvas.WX_GL_DEPTH_SIZE, 16] s.canvas = wx.glcanvas.GLCanvas(s.panel, attribList=gl_canvas_attribs, pos=(5,50)) s.context = wx.glcanvas.GLContext(s.canvas) s.canvas.SetSize((s.width,s.height)) # aggiungiamo un collegamento all'evento paint con un metodo onPaint # costruito nella nostra classe s.canvas.Bind(wx.EVT_PAINT, s.onPaint) # metodo onPaint def onPaint(s,evt): s.canvas.SetCurrent(s.context) # verifichiamo se il canvas sia stato o meno inizializzato if not s.glInizializzato: s.initGL() s.onDraw() # inizializziamo il canvas def initGL(s): if s.glInizializzato: return s.glInizializzato = True # impostiamo il colore dello sfondo glClearColor(1, 1, 1, 1) # creiamo il metodo onDraw def onDraw(s, *args, **kwargs): glClear(GL_COLOR_BUFFER_BIT) s.SwapBuffers() # ripulisci il buffer def SwapBuffers(s): s.canvas.SwapBuffers() if __name__ == "__main__": app = wx.App(False) frame = Applicazione(None, "Disegnatore") app.MainLoop() |
Faccio notare che il metodo glClearColor(1, 1, 1, 1) imposta il colore dello sfondo su bianco, mentre il metodo glClearColor(0, 0, 0, 1) lo imposta su nero. I primi tre parametri sono i valori di RGB da 0 a 1.
Siamo arrivati a buon punto e siamo praticamente pronti a disegnare il nostro poligono. Il nostro riferimento è uno spazio cartesiano con gli assi che attraversano a metà il canvas e il punto (0, 0) al centro del canvas stesso. Un poligono regolare ha tanti vertici quanti i lati e ogni vertice poggia su una circonferenza di raggio r.
Questo significa che un angolo α che passa da un vertice all’altro è dato dalla seguente equazione:
Dove n è il numero di lati (o vertici) del poligono. Traduciamo questa formula in Python nel modo seguente:
|
1 |
angolo_lato = 2.0*math.pi/s.n |
Avremo bisogno della libreria math che importiamo con:
|
1 |
import math |
L’angolo di partenza è arbitrario, però per far sì che il lato superiore del poligono sia parallelo all’asse delle ascisse voglio prendere come angolo di partenza:
Quindi la nostra formula sarà:
|
1 |
angolo_partenza = math.pi/2.0 - math.pi/s.n |
Attenzione ad inserire i numeri con almeno una cifra decimale, anche se zero, per assicurarci che Python esegua tutti i calcoli con valori decimali e non tronchi ad interi.
Infine vogliamo definire un raggio fisso per i nostri poligoni, per farlo userò come riferimento l’apotema a (anche se sarebbe sufficienti lato e raggio) nel modo seguente:
Il primo vertice avrà quindi coordinate:
Il secondo vertice sarà:
Il terzo vertice sarà:
E così via.
Traduciamo il tutto nel seguente metodo:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
def calcolaPoligono(s): apotema = 0.5 angolo_partenza = math.pi/2.0 - math.pi/s.n angolo_lato = 2.0*math.pi/s.n lato = apotema * ( 2 * math.tan(math.pi / s.n) ) raggio = math.sqrt((lato/2.0)**2+apotema**2) s.vertici = [] for a in range(s.n): s.vertici.append([raggio*math.cos(angolo_partenza+a*angolo_lato), raggio*math.sin(angolo_partenza+a*angolo_lato)]) |
Spostiamoci sul metodo onDraw e modifichiamolo nel modo seguente:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
def onDraw(s, *args, **kwargs): glClear(GL_COLOR_BUFFER_BIT) s.calcolaPoligono() glBegin(GL_POLYGON) glColor3f(1, 0.0, 0.0) for v in s.vertici: glVertex(v[0], v[1]) glEnd() s.SwapBuffers() |
Nel costruttore __init__ della classe aggiungiamo una variabile s.n per il numero di lati, subito dopo le dimensioni del canvas, nel modo seguente:
|
1 2 3 4 5 |
# stabiliamo le dimensioni del canvas s.width = 770 s.height = 500 #numero di lati s.n = 5 |
Se abbiamo fatto tutto correttamente dovremmo vedere qualcosa come questo:
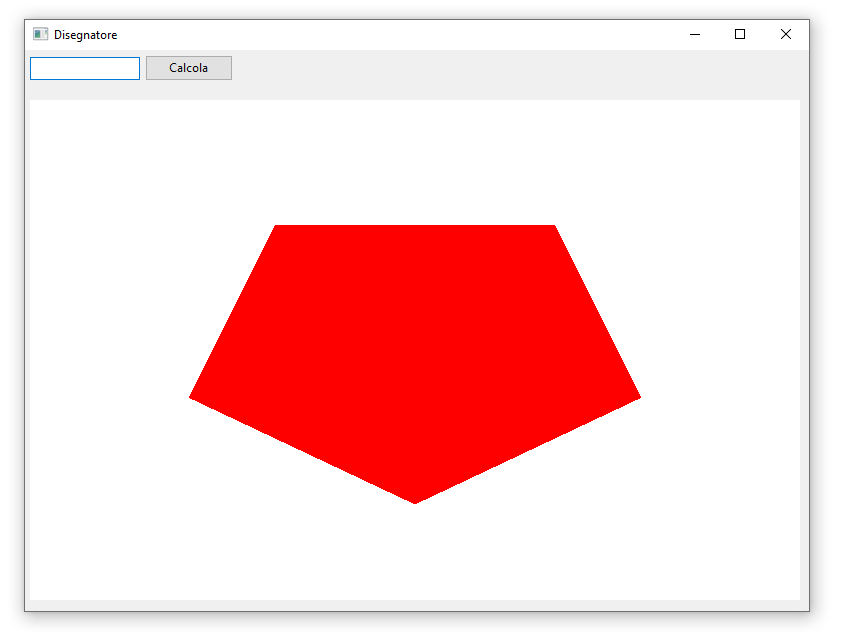
Notiamo subito che il pentagono è deformato ed inoltre manca la possibilità di definire una dimensione a piacere.
Anzitutto occupiamoci della deformazione, essa dipende dal fatto che il canvas ha una dimensione fissa di 1 x 1, che poi viene ripartita in parti decimali. Quindi tale dimensione si adatta poi alle proporzioni del canvas. Per ottenere un pentagono regolare anzitutto dobbiamo introdurre un fattore correttivo, che nel nostro caso sarà dato da:
|
1 |
s.ratio = 1.0 * s.height / s.width |
Aggiungiamo la variabile subito dopo larghezza e altezza impostate in __init__.
Modifichiamo il metodo per disegnare il poligono nel modo seguente:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
def calcolaPoligono(s): apotema = 0.5 angolo_partenza = math.pi/2.0 - math.pi/s.n angolo_lato = 2.0*math.pi/s.n lato = apotema * ( 2 * math.tan(math.pi / s.n) ) raggio = math.sqrt((lato/2.0)**2+apotema**2) s.vertici = [] for a in range(s.n): s.vertici.append([s.ratio*raggio*math.cos(angolo_partenza+a*angolo_lato), raggio*math.sin(angolo_partenza+a*angolo_lato)]) |
Adesso il poligono risulta regolare:
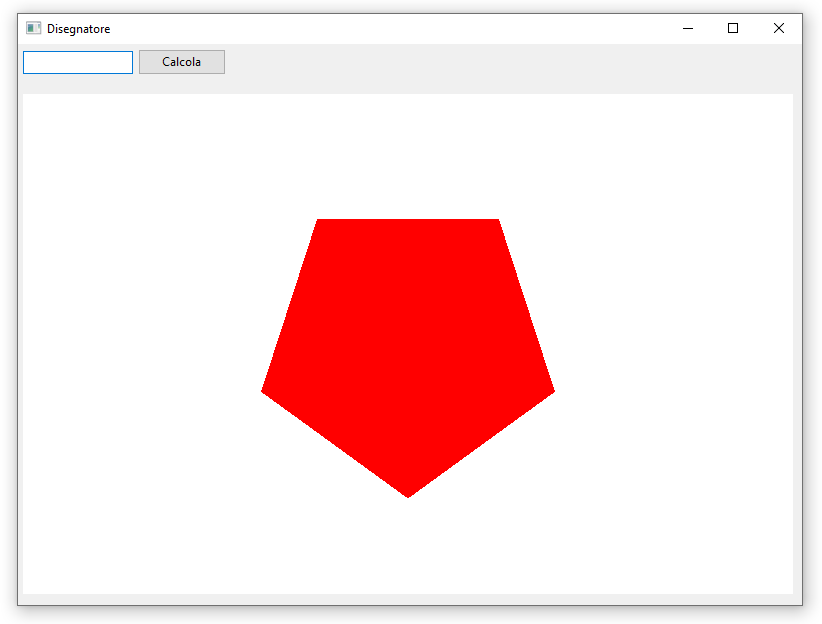
Infine attribuiamo un valore personalizzato al numero di lati s.n del poligono. Aggiungiamo i seguenti due metodi alla nostra classe:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
def btn_calcola(s,event): valore = s.testo.GetValue() if s.verificaIntero(valore): s.n = int(valore) s.Refresh() s.Update() else: wx.MessageBox(message="Inserire un valore intero da 3 a n", caption="Errore!", style=wx.OK | wx.ICON_ERROR) def verificaIntero(s,val): try: v = int(val) if v < 3: return False return True except ValueError: return False |
E dove abbiamo istanziato s.pulsante aggiungiamo:
|
1 |
s.pulsante.Bind(wx.EVT_BUTTON, s.btn_calcola) |
In questo modo colleghiamo il metodo s.btn_calcola all’evento wx.EVT_BUTTON che corrisponde alla pressione del pulsante. Con il metodo verificaIntero controlliamo se il valore passato dall’utente sia intero. Se non è intero mostriamo, grazie a wx.MessageBox, un messaggio a video con notifica di errore.
Se abbiamo fatto tutto correttamente otterremo il seguente codice finale:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 |
import wx from wx.glcanvas import GLCanvas from OpenGL.GLU import * from OpenGL.GL import * import math class Applicazione(wx.Frame): def __init__(s, parent, title): wx.Frame.__init__(s, parent, title=title, size=(800,600)) # aggiungo un panel alla classe s.panel = wx.Panel(s) # dopo il panel aggiungo i pulsanti s.aggPulsanti() # stabiliamo le dimensioni del canvas s.width = 770 s.height = 500 s.ratio = 1.0 * s.height / s.width #numero di lati s.n = 5 # aggiungiamo il controllo di inizializzazione del canvas s.glInizializzato = False # aggiungiamo il canvas, anche esso sul panel s.aggCanvas() s.Show(True) def aggPulsanti(s): # casella di testo s.testo = wx.TextCtrl(s.panel, pos=(5, 7)) # pulsante s.pulsante = wx.Button(s.panel, label="Calcola", pos=(120,5)) s.pulsante.Bind(wx.EVT_BUTTON, s.btn_calcola) def aggCanvas(s): gl_canvas_attribs = [wx.glcanvas.WX_GL_RGBA, wx.glcanvas.WX_GL_DOUBLEBUFFER, wx.glcanvas.WX_GL_DEPTH_SIZE, 16] s.canvas = wx.glcanvas.GLCanvas(s.panel, attribList=gl_canvas_attribs, pos=(5,50)) s.context = wx.glcanvas.GLContext(s.canvas) s.canvas.SetSize((s.width,s.height)) # aggiungiamo un collegamento all'evento paint con un metodo onPaint # costruito nella nostra classe s.canvas.Bind(wx.EVT_PAINT, s.onPaint) # metodo onPaint def onPaint(s,evt): s.canvas.SetCurrent(s.context) # verifichiamo se il canvas sia stato o meno inizializzato if not s.glInizializzato: s.initGL() s.onDraw() # inizializziamo il canvas def initGL(s): if s.glInizializzato: return s.glInizializzato = True # impostiamo il colore dello sfondo glClearColor(1, 1, 1, 1) # creiamo il metodo onDraw def onDraw(s, *args, **kwargs): glClear(GL_COLOR_BUFFER_BIT) s.calcolaPoligono() glBegin(GL_POLYGON) glColor3f(1, 0.0, 0.0) for v in s.vertici: glVertex(v[0], v[1]) glEnd() s.SwapBuffers() # ripulisci il buffer def SwapBuffers(s): s.canvas.SwapBuffers() def calcolaPoligono(s): apotema = 0.5 angolo_partenza = math.pi/2.0 - math.pi/s.n angolo_lato = 2.0*math.pi/s.n lato = apotema * ( 2 * math.tan(math.pi / s.n) ) raggio = math.sqrt((lato/2.0)**2+apotema**2) s.vertici = [] for a in range(s.n): s.vertici.append([s.ratio*raggio*math.cos(angolo_partenza+a*angolo_lato), raggio*math.sin(angolo_partenza+a*angolo_lato)]) def btn_calcola(s,event): valore = s.testo.GetValue() if s.verificaIntero(valore): s.n = int(valore) s.Refresh() s.Update() else: wx.MessageBox(message="Inserire un valore intero da 3 a n", caption="Errore!", style=wx.OK | wx.ICON_ERROR) def verificaIntero(s,val): try: v = int(val) if v < 3: return False return True except ValueError: return False if __name__ == "__main__": app = wx.App(False) frame = Applicazione(None, "Disegnatore") app.MainLoop() |
Se lo eseguiamo abbiamo il nostro programma che ci permetterà di disegnare qualunque poligono regolare:
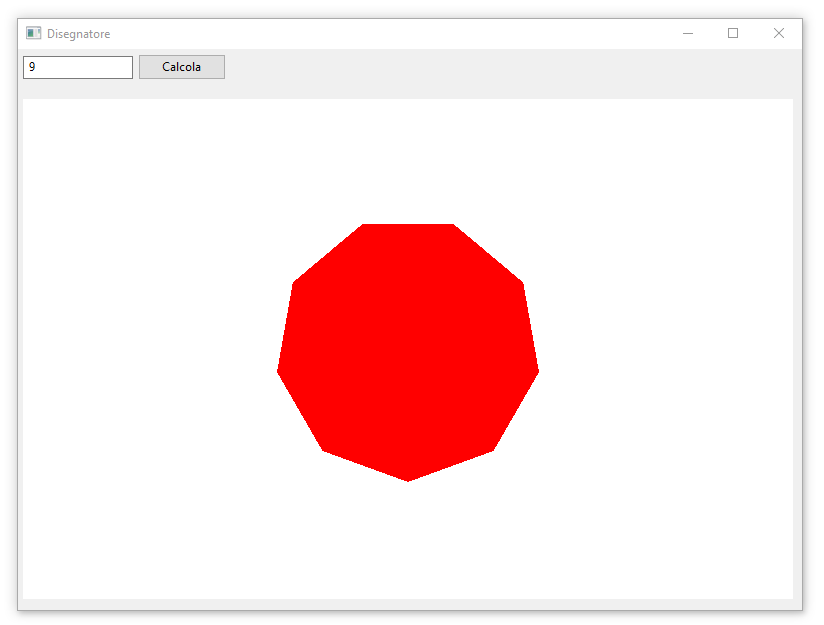

One thought on “[python] Esercizio su wxPython e PyOpenGL per disegnare un poligono dato il numero di lati”