Immaginiamo di avere la seguente situazione: su una griglia rettangolare abbiamo due punti, A e B e vogliamo calcolare il minore percorso possibile per arrivare da A a B, evitando degli ostacoli. Da una cella all’altra ci si può spostare solamente in verticale ed orizzontale.
Possiamo schematizzare il problema in qualcosa di simile.
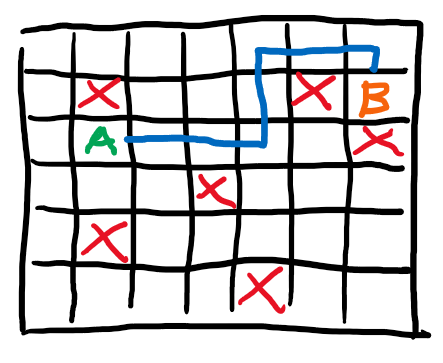
Anzitutto impostiamo le variabili necessarie:
|
1 2 3 4 5 6 7 |
n = 10 # numero di colonne m = 10 # numero di righe x = 10 # numero di ostacoli pi = [] # punto di partenza pf = [] # punto di arrivo percorsi = [] # tutti i percorsi possibili minlen = 0 # lunghezza trovata |
In particolare faccio notare che terremo tutti i percorsi in una lista percorsi = [] e vogliamo anche tenere traccia della minima lunghezza trovata con minlen. Questo accorgimento, come vedremo successivamente, ci servirà per ridurre notevolmente la quantità di calcoli da dover effettuare, eliminando tutti i percorsi che via via dovessero rivelarsi più lunghi del minimo percorso trovato (fino a quel momento).
A questo punto generiamo la matrice del mondo:
|
1 |
mtrx = [["-" for c in range(m)] for r in range(n)] |
Adesso scriviamo la funzione per popolare il mondo di blocchi, le X del disegno precedente. Per farlo utilizzeremo la libreria random, per cui ricordiamoci di importarla all’inizio con import random
|
1 2 3 4 5 6 7 8 |
def blocchi(): t = 0 while t < x: tc = random.randint(0, m-1) tr = random.randint(0, n-1) if mtrx[tr][tc] != "X": mtrx[tr][tc] = "X" t += 1 |
Utilizziamo random.randint per generare una posizione casuale su righe e colonne per i blocchi, verifichiamo che tale punto non sia già occupato da un blocco, in tal caso procediamo ad aggiungerlo.
In modo analogo creiamo un metodo che aggiunga la posizione iniziale A e quella finale B, registrandole nelle rispettive variabili.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
def inizio(): global pi, pf t = 0 while t < 2: tc = random.randint(0, m-1) tr = random.randint(0, n-1) if mtrx[tr][tc] == "-": if t == 0: mtrx[tr][tc] = "A" pi = [tr,tc] else: mtrx[tr][tc] = "B" pf = [tr,tc] t += 1 |
Per trovare il percorso procediamo nella maniera seguente:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
def trova(si,percorso=[]): # usiamo minlen come variabile globale global minlen # se la posizione corrente rientra nella matrice, allora procediamo if si[0] >= 0 and si[0] < n and si[1] >= 0 and si[1] < m: # se la posizione non e' occupata da un blocco e non e' gia' presente nel percorso procediamo if mtrx[si[0]][si[1]] != "X" and si not in percorso: # aggiungiamo la posizione percorso.append(si) # se il percorso supera la minima lunghezza trovata e tale lunghezza e' maggiore di 0, interrompiamo la ricorsione if len(percorso) > minlen and minlen > 0: return # se la posizione e' occupata dalla B allora abbiamo trovato la fine if mtrx[si[0]][si[1]] == "B": # se la lunghezza del percorso trovato e' minore della minore trovata # fino a quel momento, oppure la minore lunghezza e' a 0, aggiorniamo la lunghezza minore if len(percorso) < minlen or minlen == 0: minlen = len(percorso) #aggiungiamo il percorso ai percorsi trovati percorsi.append([]+percorso) #altrimenti eseguiamo la funzione sulle caselle circostanti else: trova([si[0]-1,si[1]],[]+percorso) trova([si[0]+1,si[1]],[]+percorso) trova([si[0],si[1]-1],[]+percorso) trova([si[0],si[1]+1],[]+percorso) |
Faccio notare una peculiarità, legata al modo in cui Python tratta le liste. Per passare il percorso attuale, copiandolo, alla funzione medesima, dobbiamo usare un piccolo trucco scrivendo []+percorso. In questo modo evitiamo che il percorso sia passato per riferimento, forzando il programma a crearne una copia.
Fatto tutto questo aggiungiamo un metodo per la stampa della matrice:
|
1 2 3 4 5 |
def stampa(): for r in mtrx: for c in r: print(c,end="") print() |
E un metodo per prendere uno dei percorsi più corti calcolati (ricordiamoci che potrebbero esserci più percorsi):
|
1 2 3 4 5 6 7 8 |
def elabora(): for p in percorsi: if len(p) == minlen: for c in p: if c != pi and c != pf: mtrx[c[0]][c[1]] = "o" print(p) break |
Infine uniamo tutto quanto insieme, importando anche la libreria temporale con import time per valutare la velocità di elaborazione.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
ti = time.time() blocchi() inizio() print("mappa senza percorso") stampa() trova(pi,[]) print("mappa con percorso") elabora() stampa() print("percorsi trovati %d" % len(percorsi)) tf = time.time() print("tempo di calcolo: %.2f s" % (tf - ti)) |
Di seguito il codice completo:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
import random import time n = 10 # numero di colonne m = 10 # numero di righe x = 10 # numero di ostacoli pi = [] # punto di partenza pf = [] # punto di arrivo percorsi = [] # tutti i percorsi possibili minlen = 0 # lunghezza trovata mtrx = [["-" for c in range(m)] for r in range(n)] def blocchi(): t = 0 while t < x: tc = random.randint(0, m-1) tr = random.randint(0, n-1) if mtrx[tr][tc] != "X": mtrx[tr][tc] = "X" t += 1 def inizio(): global pi, pf t = 0 while t < 2: tc = random.randint(0, m-1) tr = random.randint(0, n-1) if mtrx[tr][tc] == "-": if t == 0: mtrx[tr][tc] = "A" pi = [tr,tc] else: mtrx[tr][tc] = "B" pf = [tr,tc] t += 1 def stampa(): for r in mtrx: for c in r: print(c,end="") print() def trova(si,percorso=[]): # usiamo minlen come variabile globale global minlen # se la posizione corrente rientra nella matrice, allora procediamo if si[0] >= 0 and si[0] < n and si[1] >= 0 and si[1] < m: # se la posizione non e' occupata da un blocco e non e' gia' presente nel percorso procediamo if mtrx[si[0]][si[1]] != "X" and si not in percorso: # aggiungiamo la posizione percorso.append(si) # se il percorso supera la minima lunghezza trovata e tale lunghezza e' maggiore di 0, interrompiamo la ricorsione if len(percorso) > minlen and minlen > 0: return # se la posizione e' occupata dalla B allora abbiamo trovato la fine if mtrx[si[0]][si[1]] == "B": # se la lunghezza del percorso trovato e' minore della minore trovata # fino a quel momento, oppure la minore lunghezza e' a 0, aggiorniamo la lunghezza minore if len(percorso) < minlen or minlen == 0: minlen = len(percorso) #aggiungiamo il percorso ai percorsi trovati percorsi.append([]+percorso) #altrimenti eseguiamo la funzione sulle caselle circostanti else: trova([si[0]-1,si[1]],[]+percorso) trova([si[0]+1,si[1]],[]+percorso) trova([si[0],si[1]-1],[]+percorso) trova([si[0],si[1]+1],[]+percorso) def elabora(): for p in percorsi: if len(p) == minlen: for c in p: if c != pi and c != pf: mtrx[c[0]][c[1]] = "o" print(p) break ti = time.time() blocchi() inizio() print("mappa senza percorso") stampa() trova(pi,[]) print("mappa con percorso") elabora() stampa() print("percorsi trovati %d" % len(percorsi)) tf = time.time() print("tempo di calcolo: %.2f s" % (tf - ti)) |
L’output finale darà qualcosa di simile a questo:


One thought on “[python] Esercizio su funzioni ricorsive e calcolo del percorso minore possibile”